*this' clause is removed. Heading corrections. Formatting corrections.*this") to match current standard ie. "T shall be
Cpp17MoveInsertable into hive" becomes "T is Cpp17MoveInsertable into
*this". Added "This operation may change capacity()" to
remarks in reshape. sort: Throws section removed as this is covered by
blanket wording and by Remarks and the post-Remarks note. Specifically the
following line is removed: "Throws: bad_alloc if it fails to
allocate any memory necessary for this operation. comp may
also throw." Note: forward_list::sort and list::sort do not include such a
line.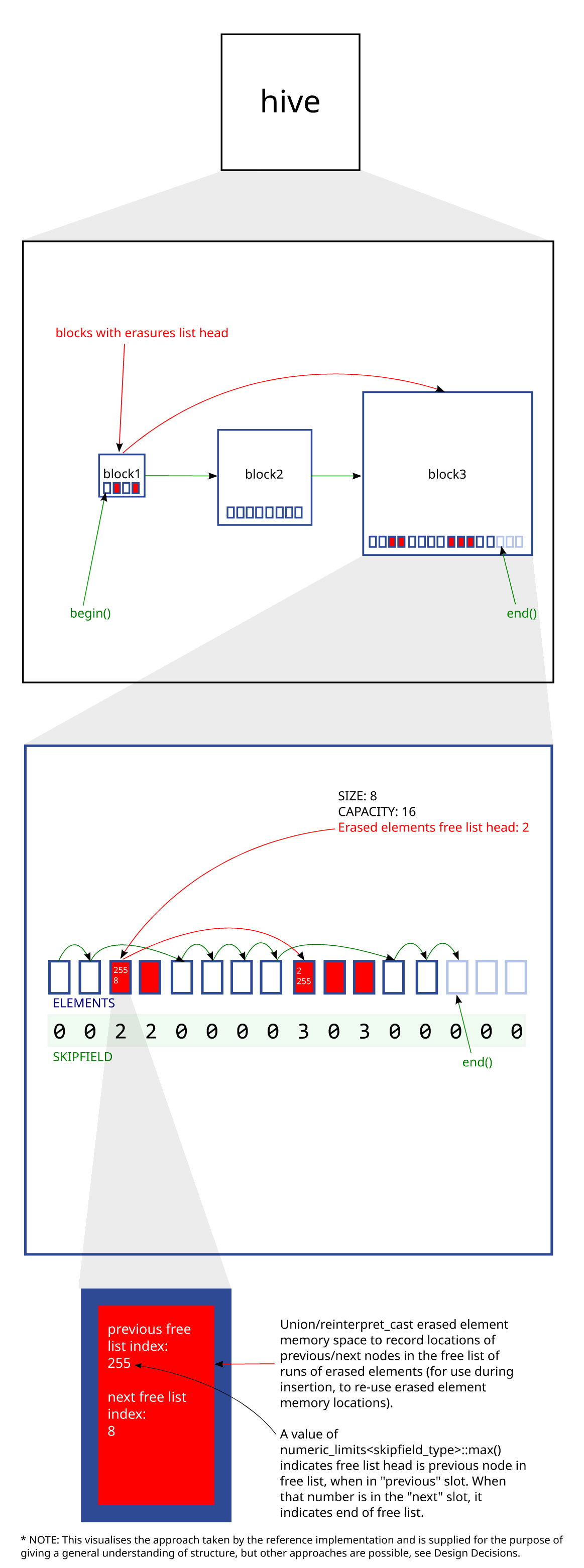
The purpose of a container in the standard library cannot be to provide the optimal solution for all scenarios. Inevitably in fields such as high-performance trading or gaming, the optimal solution within critical loops will be a custom-made one that fits that scenario perfectly. However, outside of the most critical of hot paths, there is a wide range of application for more generalized solutions.
Hive is a formalisation, extension and optimization of what is typically known as a 'bucket array' or 'object pool' container in game programming circles. Thanks to all the people who've come forward in support of the paper over the years, I know that similar structures exist in various incarnations across many fields including high-performance computing, high performance trading, 3D simulation, physics simulation, robotics, server/client application and particle simulation fields (see this google groups discussion, the hive supporting paper #1 and appendix links to prior art).
The concept of a bucket array is: you have multiple memory blocks of elements, and a boolean token for each element which denotes whether or not that element is 'active' or 'erased' - commonly known as a skipfield. If it is 'erased', it is skipped over during iteration. When all elements in a block are erased, the block is removed, so that iteration does not lose performance by having to skip empty blocks. If an insertion occurs when all the blocks are full, a new memory block is allocated.
The advantages of this structure are as follows: because a skipfield is used, no reallocation of elements is necessary upon erasure. Because the structure uses multiple memory blocks, insertions to a full container also do not trigger reallocations. This means that element memory locations stay stable and iterators stay valid regardless of erasure/insertion. This is highly desirable, for example, in game programming because there are usually multiple elements in different containers which need to reference each other during gameplay, and elements are being inserted or erased in real time. The only non-associative standard library container which also has this feature is std::list, but it is undesirable for performance and memory-usage reasons. This does not stop it being used in many open-source projects due to this feature and it's splice operations.
Problematic aspects of a typical bucket array are that they tend to have a
fixed memory block size, tend to not re-use memory locations from erased
elements, and utilize a boolean skipfield. The fixed block size (as opposed to
block sizes with a growth factor) and lack of erased-element re-use leads to
far more allocations/deallocations than is necessary, and creates memory waste
when memory blocks have many erased elements but are not entirely empty. Given
that allocation is a costly operation in most operating systems, this becomes
important in performance-critical environments. The boolean skipfield makes
iteration time complexity at worst O(n) in capacity(), as there is
no way of knowing ahead of time how many erased elements occur between any two
non-erased elements. This can create variable latency during iteration. It also
requires branching code for each skipfield node, which may cause performance
issues on processors with deep pipelines and poor branch-prediction failure
performance.
A hive uses a non-boolean method for skipping erased elements, which allows for more-predictable iteration performance than a bucket array and O(1) iteration time complexity; the latter of which means it meets the C++ standard requirements for iterators, which a boolean method doesn't. It has an (optional - on by default) growth factor for memory blocks and reuses erased element locations upon insertion, which leads to fewer allocations/reallocations. Because it reuses erased element memory space, the exact location of insertion is undefined. Insertion is therefore considered unordered, but the container is sortable. Lastly, because there is no way of predicting in advance where erasures ('skips') may occur between non-erased elements, an O(1) time complexity [ ] operator is not possible and thereby the container is bidirectional but not random-access.
There are two patterns for accessing stored elements in a hive: the first is to iterate over the container and process each element (or skip some elements using advance/prev/next/iterator ++/-- functions). The second is to store an iterator returned by insert() (or a pointer derived from the iterator) in some other structure and access the inserted element in that way. To better understand how insertion and erasure work in a hive, see the following diagrams.
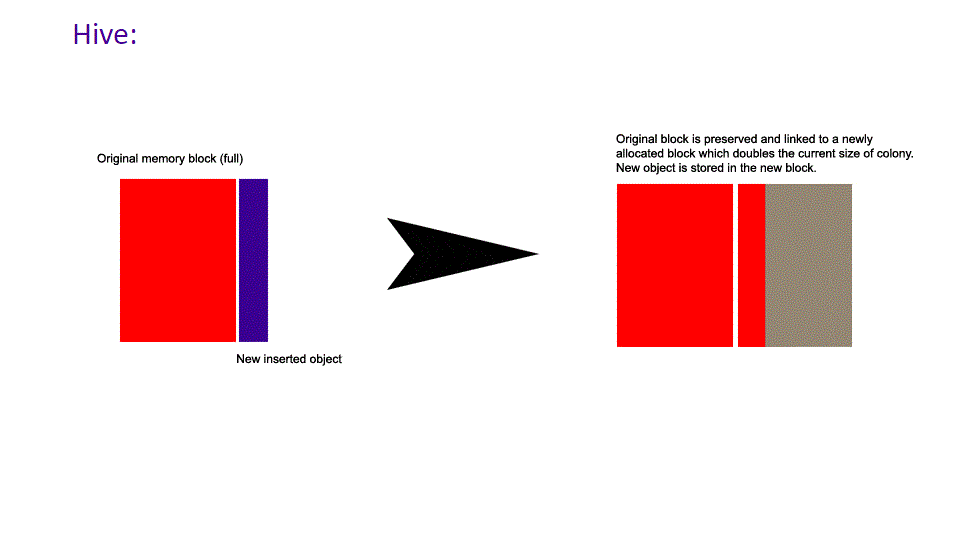
The following demonstrates how insertion works in a hive compared to a vector when size == capacity.

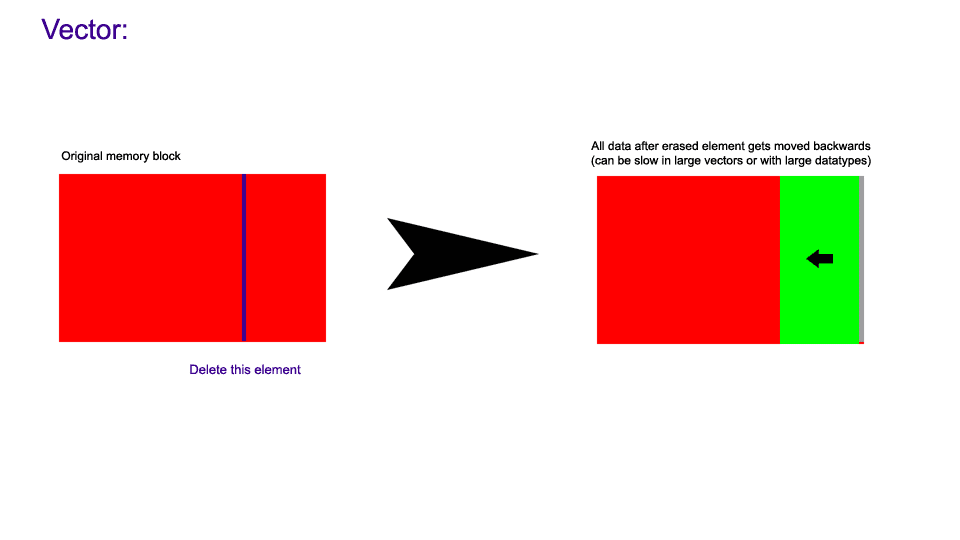
The following images demonstrate how non-back erasure works in a hive compared to a vector.

There is additional introductory information about the container's structure in this CPPcon talk, though much of it's information is out of date (hive no longer uses a stack but a free list instead, benchmark data is out of date, etcetera), and more detailed implementation information is available in this CPPnow talk. Both talks discuss the precursor for std::hive, called plf::colony.
For the purposes of the non-technical-specification sections of this document, the following terms are defined:
There are situations where data is heavily interlinked, iterated over frequently, and changing often. An example is the typical video game engine. Most games will have a central generic 'entity' or 'actor' class, regardless of their overall schema (an entity class does not imply an ECS). Entity/actor objects tend to be 'has a'-style objects rather than 'is a'-style objects, which link to, rather than contain, shared resources like sprites, sounds and so on. Those shared resources are usually located in separate containers/arrays so that they can re-used by multiple entities. Entities are in turn referenced by other structures within a game engine, such as quadtrees/octrees, level structures, and so on.
Entities may be erased at any time (for example, a wall gets destroyed and no longer is required to be processed by the game's engine, so is erased) and new entities inserted (for example, a new enemy is spawned). While this is all happening the links between entities, resources and superstructures such as levels and quadtrees, must stay valid in order for the game to run. The order of the entities and resources themselves within the containers is, in the context of a game, typically unimportant, so an unordered container is okay. More specific requirements for game engines are listed in the appendices.
But the non-fixed-size container with the best iteration performance in the standard library, vector, loses pointer validity to elements within it upon insertion, and pointer/index validity upon erasure. This leads towards sophisticated and often restrictive workarounds when developers attempt to utilize vector or similar containers under the above circumstances.
std::list and the like are not suitable due to their poor memory locality, which leads to poor cache performance during iteration. This does not stop them from being used extensively. This is however an ideal situation for a container such as hive, which has a high degree of memory locality. Even though that locality can be punctuated by gaps from erased elements, it still works out better in terms of iteration performance than all other standard library containers other than deque/vector, regardless of the ratio of erased to non-erased elements (see benchmarks). It is also in most cases faster for insertion and (non-back) erasure than current standard library containers.
As another example, particle simulation (weather, physics etcetera) often involves large clusters of particles which interact with external objects and each other. The particles each have individual properties (eg. spin, speed, direction etc) and are being created and destroyed continuously. Therefore the order of the particles is unimportant, what is important is the speed of erasure and insertion. No current standard library container has both strong insertion and non-back erasure performance, so again this is a good match for hive.
Reports from other fields suggest that, because most developers aren't aware of containers such as this, they often end up using solutions which are sub-par for iterative performance such as std::map and std::list in order to preserve pointer validity, when most of their processing work is actually iteration-based. So, introducing this container would both create a convenient solution to these situations, as well as increasing awareness of this approach. It will ease communication across fields, as opposed to the current scenario where each field uses a similar container but each has a different name for it (object pool, bucket array, etcetera).
This is purely a library addition, requiring no changes to the language.
The three core aspects of a hive from an abstract perspective are:
Each element block houses multiple elements. The metadata about each block may or may not be allocated with the blocks themselves and could be contained in a separate structure. This metadata must include at a minimum, the number of non-erased elements within each block and the block's capacity - which allows the container to know when the block is empty and needs to be removed from the sequence, and also allows iterators to judge when the end of a block has been reached, given the starting point of the block.
It should be noted that most of the data associated with the skipping mechanism and erased-element recording mechanisms should be per-element-block and independent of subsequent/previous element blocks, as otherwise you would create unacceptably variable latency for any fields involving timing sensitivity. Specifically with a global data set for either, erase would likely require all data subsequent to a given element block's data to be reallocated, when an element block is removed from the iterative sequence. Insert would likewise require reallocation of all data to a larger memory space when hive capacity expanded.
In the original reference implementation (current reference implementation is here) the specific structure and mechanisms have changed many times over the course of development, however the interface to the container and its time complexity guarantees have remained largely unchanged. So it is likely that regardless of specific implementation, it will be possible to maintain this interface without obviating future improvement.
The current reference implementation implements the 3 core aspects as follows. Information about known alternative ways to implement these is available in the appendices.
In the reference implementation this is essentially a doubly-linked list of 'group' structs containing (a) a dynamically-allocated element block, (b) element block metadata and (c) a dynamically-allocated skipfield. The element blocks and skipfields have a growth factor of 2. The metadata includes information necessary for an iterator to iterate over hive elements, such as that already mentioned and information useful to specific functions, such as the group's sequence order number (used for iterator comparison operations). This linked-list approach keeps the operation of removing empty element blocks from the sequence at O(1) time complexity.
The reference implementation uses a skipfield pattern called the low complexity jump-counting pattern. This encodes the length of runs of contiguous erased elements (skipblocks) into a skipfield which allows for O(1) time complexity during iteration (see the paper above for details). Since there is no branching involved in iterating over the skipfield aside from end-of-block checks, it is less problematic computationally than a boolean skipfield (which has to branch for every skipfield read) in terms of CPUs which don't handle branching or branch-prediction failure efficiently (eg. Core2).
The reference implementation utilizes the memory space of erased elements to form a per-element-block index-based
doubly-linked free list of skipblocks, which is used during subsequent insertion.
Each element block has a 'free list head' as a metadata member. The free lists are index-based rather
than pointer-based in order to reduce the amount of space necessary to store
the 'previous' and 'next' list links in an erased element's memory. The
beginning and end of the free lists are marked using
numeric_limits<skipfield_type>::max() in the 'previous'
and 'next' indexes, respectively. If the free list head is equal to this number
this means there are no erasures in that element block. Since this number is reserved that means element block capacities cannot be larger than numeric_limits<skipfield_type>::max() ie. 255 elements instead of 256 for 8-bit skipfield types, as otherwise the free list would be unable to address a skipblock comprised only of the last element in the block.
These per-element-block free lists are combined with a doubly-linked pointer-based intrusive list of blocks with erased elements in them, the head of which is stored as a member variable in hive. The combination of these two things allows re-use of erased element memory space in O(1) time.
More information on these approaches, and alternative approaches to the 3 core aspects, is available to read in the alt implementation appendix.
Iterators are bidirectional in hive but also provide constant time
complexity >, <, >=, <= and <=> operators for convenience
(eg. in for loops when skipping over multiple elements per loop
and there is a possibility of going past a pre-determined end element). This is
achieved by keeping a record of the relative order of element blocks. In the
reference implementation this is done by assigning a number to each memory
block in its metadata. In an implementation using a vector of pointers to
groups instead of a linked list, one can simply use the position of the
pointers within the vector to determine this. Comparing the relative order of
two iterators' blocks, then comparing the memory locations of the elements
which the iterators point to (if they happen to be within the same memory
block), is enough to implement all comparisons.
Iterator implementations are dependent on the approach taken to core aspects 1 and 2 as described above. The reference implementation's iterator stores a pointer to the current 'group' struct, plus a pointer to the current element and a pointer to its corresponding skipfield node. It is possible to replace the element and skipfield pointers with a single index value, but benchmarks have shown this to be slower despite the increased memory cost.
The reference implementation's ++ operation is as shown below, following the low-complexity jump-counting pattern's algorithm:
-- operation is the same except both step 1 and 2 involve subtraction rather than addition and step 3 checks to see if the element pointer is now before the beginning of the element block instead of beyond the end of it. If it is before the beginning of the block it traverses to the back element of the previous group's element block, and subtracts the value of the back skipfield node from the element pointer and skipfield pointer.
We can see from the above that every so often iteration will involve a transistion to the next/previous element block in the hive's sequence of active blocks, depending on whether we are doing ++ or --. Hence for every element block transition, 2 reads of the skipfield are necessary instead of 1.
advance, prev and nextFor these functions, complexity is dependent on the state of the hive instance, position of the iterator and the amount of distance to travel, but in many cases will be less than linear, and may be constant. To explain: it is necessary in a hive to store, for each element block, both capacity metadata (for the purpose of iteration) and metadata about how many non-erased elements are present (ie. size, for the purpose of removing blocks from the iterative chain once they become empty). For this reason, intermediary blocks between the iterator's initial block and its final destination block (if these are not the same block, and are not immediately adjacent) can be skipped rather than iterated linearly across, by using the size metadata.
This means that the only linear time operations are any iterations within the initial block and the final block. However if either the initial or final block have no erased elements (as determined by comparing whether the block's capacity and size metadata are equal), linear iteration can be skipped for that block and pointer/index math used instead to determine distances, reducing complexity to constant time. Finally, if the iterator points to the first element in that element block, and distance is greater-or-equal-to the block's size, we can treat it as an intermediary block and just skip it, subtracting size from the distance we want to travel. Hence the best case for this operation is constant time, the worst is linear in the distance.
distance(first, last)The same considerations which apply to advance, prev and next also apply to distance - intermediary element blocks between first and last's blocks can be skipped in constant time and their size metadata added to the cumulative distance count, while first's block and last's block (if they are not the same block) must be linearly iterated across unless either block has no erased elements, in which case the operation becomes pointer/index math and is reduced to constant time for that block. If first and last are in the same block but are in the first and last element slots in the block, distance can again be calculated from the block's size metadata in constant time. If they are not in the same block but first points to the first element in it's block, the first block can be skipped and it's size added to the distance travelled. Likewise if last points to the last element in it's block, the last block can also be skipped and it's size added.
iterator insert/emplaceInsertion can re-use previously-erased element memory locations when available, so position of insertion is effectively random unless no previous erasures have occurred, in which case all elements will likely be inserted linearly to the back of the container in the majority of implementations. If inserting to the back this invalidates iterators pointing to end(). It could also potentially insert before begin(), if erasures have occurred at the beginning of the container.
While it is not mandated to do so, hive implementations will generally insert into existing element blocks when able, and create a new element block only when all existing element blocks are full.
If hive is implemented as a vector of pointers to element blocks instead of a linked list of element blocks, creation of a new element block would occasionally involve expanding the pointer vector, itself O(n) in the number of blocks, but this is within amortized limits since it is only occasional.
void insertFor range, fill and initializer_list insertion, it is not possible to guarantee that all the elements inserted will be sequential in the hive's sequence, and so it is not considered useful to return an iterator to the first inserted element. There is a precedent for this in the various std:: map containers. Therefore these functions return void.
The same considerations regarding iterator invalidation in singular insertion above, also applies to these insertion styles.
For multiple insertions an implementation can call reserve() in advance, reducing the number of allocations necessary (whereas repeated singular insertions would generally follow the implementation's block growth factor, and possibly allocate more and smaller element blocks than necessary). This has no effect on time complexity which is still linear in the number elements inserted.
iterator erase(const_iterator
position)Erasure is a simple matter of destructing the element in question and updating whatever data is associated with the erased-element skipping mechanism. No reallocation of subsequent elements is necessary and hence the process is O(1). Updates to the erased-element recording and skipping mechanisms are also required to be O(1).
When an element block becomes empty of non-erased elements it must be freed to the OS (or reserved for future insertions, depending on implementation) and removed from the hive's sequence of active blocks. If it were not, we would end up with non-O(1) iteration, since there would be no way to predict how many empty element blocks were between the current element block being iterated over, and the next element block with non-erased elements in it.
In a linked-list-of-blocks style of implementation this removal is always O(1). However if the hive were implemented as vector of pointers to element blocks, this could, depending on implementation, trigger an O(n) relocation of subsequent block pointers in the vector (a smart implementation would only do this occasionally, using erase_if - see the alt implementation appendix). Hence this operation is O(1) amortized.
Under what circumstances element blocks are reserved rather than deallocated is implementation-defined - however given that small memory blocks have low cache locality compared to larger ones, from a performance perspective it is best to only reserve the largest blocks currently allocated in the hive. In my benchmarking, reserving both the back and 2nd-to-back element blocks while ignoring the actual capacity of the blocks themselves seemed to have the most beneficial performance characteristics out of other techniques attempted.
There are three main performance advantages to retaining back blocks as opposed to just any block - the first is that these will be, under most circumstances, the largest blocks in the hive (given the growth factor). An exception to this is when splice is used, which may result in a smaller block following a larger block (implementation-dependent). The second advantage is that in situations where erasures and insertions are occurring at the back of the hive (this assumes no erased element locations in other memory blocks, which would most likely be used for the insertions) continuously and in quick succession, retaining the back block avoids large numbers of deallocations/reallocations. The third advantage is that deallocations of these larger blocks can, in part, be moved by the user to non-critical code regions via trim_capacity(). Though ultimately if the user wants total control of when allocations and deallocations occur they would need to use a custom allocator.
Lastly, the reason for returning an iterator is: if an erasure empties an element block of elements, the block will be deallocated or reserved - in either case, it's no longer part of the iterative sequence and an iterator pointing into it, such as position, can no longer be used for iteration. This is important for erasing inside a loop.
iterator erase(const_iterator first,
const_iterator last)The same considerations for singular erasure above also apply for range-erasure. In addition, ranged erasure is O(n) if elements are non-trivially-destructible. If they are trivially-destructible, we can follow similar logic to the distance specialization above. Which is to say, for the first and last element blocks in the range, if the number of elements in either block are equal to their capacity, there are no erasures in the block and we may be able to - depending on the erased-element-skipping-mechanism - simply notate a new skipblock without needing to deal with any existing skipblocks. If there are erasures in that element block, we would (implementation-dependent) likely need to identify whether the range we're erasing contains erased elements in between the non-erased elements, in order to update metadata (such as number of non-erased elements in the block) correctly.
For intermediary blocks between the first and last blocks, for trivially-destructible types we can simply deallocate or reserve these without calling the destructors of elements or dealing with the erased-element skipping/recording mechanisms for those blocks. As with distance, if the first iterator points to the first element in it's element block, the first block can be treated like an intermediary block - likewise for the last block, if the last iterator points to the last element in it's element block. Hence for trivially-destructible types, the entire operation can be linear in the number of blocks contained within the range or linear in the number of elements contained within the range, or somewhere in between.
As with singular erasure, in a vector-of-pointers-to-blocks style of implementation, there may be a need to reallocate element block pointers backward when blocks becomes empty of elements.
Lastly, specifying a return iterator for range-erase may seem pointless,
as no reallocation of elements occurs in erase for hive, so the return
iterator will almost always be the last const_iterator of the
first, last pair. However if
last was end(), the new value of
end() will be
returned. In this case either the user intentionally submitted end() as
last, or they incremented an iterator pointing to the final
element in the hive and submitted that as last. The latter is
the only valid reason to return an iterator from the function, as it may
occur as part of a loop which is erasing elements which ends when
end() is reached. If end() is changed by the
erasure, but the iterator used in the loop
does not accurately reflect end()'s new value, that iterator
could iterate past end() and the loop would never end.
void reshape(std::hive_limits
block_limits)This function updates the block capacity limits in the hive with user-defined ones and, if necessary, changes any active blocks which fall outside of those limits to be within the limits (and deallocates any reserved blocks outside of the limits - although an implementation could choose to allocate new reserved blocks if they wanted). A program will not compile if the function is used with non-copyable/movable types. It will invalidate pointers/iterators/references to if reallocation of elements to other element blocks occurs.
The order of elements post-reshape is not guaranteed to be stable, in order to allow for optimizations. Specifically: in the instance where a given element element block does not fit within the limits supplied, the elements within that element block could be reallocated to previously-erased element locations in other element blocks which do fit within the limits supplied. Or they could be reallocated to the back of the final element block, if it fits within the limits, or into reserved blocks if they fit within the limits.
If the existing current limits fit within the new user-supplied ones, no
checking of block capacities is needed and the operation is O(1).
If they do not but existing blocks may fit within the limits, all blocks
need to be checked, making the operation O(n) in the number of blocks (both
active and reserved). If any blocks containing elements don't fit within
the supplied limits reallocation will occur and the operation is at worst O(n) in
capacity().
static constexpr std::hive_limits
block_capacity_hard_limits() noexceptAs opposed to block_capacity_limits() which returns the current min/max element block capacities for a given instance of hive, this allows the user to get any implementation's min/max 'hard' lower/upper limits for element block capacities ie. the limits which any user-supplied limits must fit within. For example, if an implementation's hard limit is 3 elements min, 1 million elements max, all user-supplied limits must be >= 3 and <= 1 million.
This is useful for 2 reasons:
void clear()User expectation was that clear() would erase all elements but not deallocate element blocks. Therefore all active blocks are emptied of elements and become reserved blocks. If deallocation of memory blocks is desired, a clear() call can be followed by a trim_capacity() call. For trivially-destructible types element destruction can be skipped and depending on implementation the process may be O(1).
iterator get_iterator(const_pointer p) noexcept
const_iterator get_iterator(const_pointer p) const noexceptBecause hive iterators could be large, potentially storing three
pieces of data - eg. pointers to: current element block, current element
and current skipfield node - a program storing many links to
elements within a hive may opt to dereference iterators to get pointers and
store those instead of iterators, to save memory and improve performance
via reduced cache use. This function reverses that process, giving an
iterator which can then be used for operations such as erase.
A get_const_iterator function was fielded as a workaround for the
possibility of someone wanting to supply a non-const pointer and get a
const_iterator back, however as_const fulfills this same role
when supplied to get_iterator and doesn't require expanding
the interface of hive. Likewise it was decided to use const_pointer's because if a user wants to supply a non-const pointer they can use as_const,
whereas there is no meaningful equivalent process to convert const_pointer to pointer.
Note that this function is only guaranteed to return an iterator that
corresponds to the pointer supplied - it makes no checks to see whether the
element which p originally pointed to is the same element
which p now points to (eg. from an ABA scenario). Resolving
this problem is down to the end user and could involve having a unique id
within elements or similar (more info in the frequently-asked questions appendix).
Technically, a precondition of the function is that p points to an
element in *this, and does not point to an erased element, otherwise behaviour is undefined. This is
due to the "lifetime
pointer zap" issue ie. reading the value of a pointer to an erased
element is undefined behaviour in C++. In practice this is usually non-problematic and many fields are fine with this situation. The reference implementation returns
end() when p is not an element in
*this and it is possible that other implementations may do the
same. LEWG decided to remove this as an Effect of the function due to the
UB mentioned.
Note 1: in order to check whether a given element is erased when an implementation is using the low-complexity jump-counting pattern, the additional operations specified under "Parallel processing" in that paper must be followed.
Note 2: get_iterator compares pointers against the start and end
memory locations of the active blocks in
*this. There was some confusion that this would be problematic
due to obscure rules in the standard which state that a given platform may
allow addresses inside of a given memory block to essentially not be
contiguous, at least in terms of the std::less/std::greater/>/</etc
operators. According to Jens Maurer, these difficulties can be bypassed via
hidden channels between the library implementation and the compiler.
void shrink_to_fit()A decision had to be made as to whether this function should, in the
context of hive, be allowed to reallocate elements (as std::vector
implementations tend to do) or simply trim off reserved blocks (as
std::deque implementations tend to do). Due to the fact that a large hive
memory block could have as few as one remaining element in a large active
block after a series of erasures, it makes little sense to only trim reserved
blocks, so instead a shrink_to_fit reallocates all elements to
as few active blocks as possible in order to increase cache locality during
iteration and reduce memory usage. It cannot guarantee that size() ==
capacity() after the operation, because the min/max block capacity
limits of *this may prevent that.
One potential implementation is fairly brute-force - create a new temporary hive, reserve(size() of original hive), copy/move all elements from the original hive into the temporary, then operator = && the temporary into the original. A more astute implementation might allocate a temporary array detailing the full capacity and unused capacity of each block, then use some procedure to move elements out of some blocks and into as few of the existing blocks as possible, filling up any erased element locations and/or unused space at the back of the hive and only allocating new element blocks as-necessary. The latter approach is why the order of elements post-reshape is not guaranteed to be stable.
void trim_capacity()
void trim_capacity(size_type n)The trim_capacity() command was also introduced as a way to free reserved blocks which had been previously created via reserve() or
transformed from active blocks to reserved blocks via erase(), without
reallocating elements and invalidating iterators as shrink_to_fit() does.
The second overload was introduced as a way of allowing the user to say "I
want to retain at least n capacity while freeing reserved blocks, so that I
have room for future insertions without having to allocate again". This
means the user doesn't have to know how much unused capacity is in (a)
unused element memory space in the back block, (b) unused
element memory space from prior erasures, or (c) reserved blocks. They
just say how much they want to retain, and the implementation will free as
much of the the remainder (capacity() - n) as possible if
there are suitable reserved blocks available to deallocate.
void sort()Although the container has unordered insertion, there may be circumstances where sorting is desired. Because hive uses bidirectional iterators, using std::sort or other random access sort techniques is not possible. Therefore an internal sort routine is supplied, bringing it in line with std::list. An implementation of the sort routine used in the reference implementation of hive can be found in a non-container-specific form here - see that page for the technique's advantages over the usual sort algorithms for non-random-access containers. An allowance is made for sort to allocate memory if necessary, so that algorithms such as this can be used. Since memory allocation is unspecified but allowed for std::list::sort/std::forward_list::sort, this is not necessary, just courtesy.
void unique();
template <class BinaryPredicate>
size_type unique(BinaryPredicate binary_pred); Likewise, if a container can be sorted, unique() may be of use post-sort. Optimal implementation of unique involves calling the range-erase function where possible, as range-erase has potentially constant time depending on the state of the given blocks, as opposed to calling single-element erase() repeatedly which would be at worst O(n - 1).
void splice(hive &x)
void splice(hive &&x) *this
+ the number of blocks in x)
Whether x's active blocks are transferred to the beginning
or end of *this's sequence of active blocks, or interlaced in
some way (for example to order blocks by their capacity from small to
large) is implementation-defined. Better performance may be gained in some
cases by allowing the source's active blocks to go to the front rather than
the back, depending on how full the final active block in x
is. This is because unused elements that are not at the back of hive's
iterative sequence will need to be marked as skipped in some way, and
skipping over large numbers of elements will incur a small performance
disadvantage during iteration compared to skipping over a small number of
elements, due to memory locality.
This function may throw in three ways - the first is a
length_error exception if any of the capacities of
x's active blocks are outside of *this's block capacity
limits. The second is an exception if the allocators of the
two hives are different. Third is a potential bad_alloc in the case of a
vector-of-pointers-to-blocks style of implementation, where an
allocation may be made if *this's pointer vector isn't of
sufficient capacity to accomodate the pointers to x's active blocks.
For that scenario the time complexity (to expand the vector and reallocate all pointers) is linear in the number of the element blocks in *this + the number of active blocks in x. But regardless of implementation, a check needs to be
made as to whether the x's active blocks are within *this's current block limits. This check may be O(1) or O(n) in the number of x's active blocks depending on the values of *this's and x's current limits (same logic as reshape() above).
Final note: reserved blocks in x are not transferred into *this. This was decided by LEWG to be non-implementation defined in
order to not create unexpected behaviour when moving from one implementation to another. An implementation may need to count the amount of capacity stored in reserved blocks in the two hive instances in order to correct the total capacity values of both, which may involve a traversal of reserved blocks.
Suggested location of hive in the standard is Sequence Containers.
#define __cpp_lib_hive <editor supplied value> // also in
<hive>
| Subclause | Header |
| Requirements | |
| Sequence containers | <array>, <deque>, <forward_list>, <list>, <vector>, <hive> |
| Associative containers | <map>, <set> |
| Unordered associative containers | <unordered_map>, <unordered_set> |
| Container adaptors | <queue>, <stack> |
| Views | <span> |
<hive> synopsis [hive.syn]
#include <initializer_list> // see [initializer.list.syn]
#include <compare> // see [compare.syn]
namespace std {
// class template hive
struct hive_limits;
template <class T, class Allocator = allocator<T>> class hive;
template<class T, class Allocator>
void swap(hive<T, Allocator>& x, hive<T, Allocator>& y)
noexcept(noexcept(x.swap(y)));
template<class T, class Allocator, class U>
typename hive<T, Allocator>::size_type
erase(hive<T, Allocator>& c, const U& value);
template<class T, class Allocator, class Predicate>
typename hive<T, Allocator>::size_type
erase_if(hive<T, Allocator>& c, Predicate pred);
namespace pmr {
template <class T>
using hive = std::hive<T, polymorphic_allocator<T>>;
}
}
hive [hive]erase or clear -
end example] are either deallocated or become reserved blocks. Reserved
blocks can be allocated by the user [Example: by reserve - end
example] for future use during insertions, at which point they become
active blocks.(5.1) — The minimum limit shall be no larger than the maximum limit.
(5.2) — When limits are not specified by a user during construction, the implementation's default limits are used.
(5.3) — The default limits of an implementation are not guaranteed to be the same as the minimum and maximum possible capacities for an implementation's element blocks [Note 1: To allow latitude for both implementation-specific and user-directed optimization. - end note]. The latter are defined as hard limits.
(5.4) — If user-specified limits are not within hard limits, or if the specified minimum limit is greater than the specified maximum limit, behavior is undefined.
(5.5) — After construction a hive's
limits can be changed by the user via reshape.
(5.6) — Limits are copied between
hives during copy construction, move construction, operator = (hive
&&) and swap.
(5.7) — An element block is said to be within the bounds of a pair of minimum/maximum limits when it's capacity is >= the minimum limit and <= the maximum limit.
== and !=. A hive also meets
the requirements of a reversible container ([container.rev.reqmts]), of an
allocator-aware container ([container.alloc.reqmts]), and some of the
requirements of a sequence container, including several of the optional
sequence container requirements ([sequence.reqmts]). Descriptions are
provided here only for operations on hive that are not described in that
table or for operations where there is additional semantic information.namespace std {
struct hive_limits
{
size_t min;
size_t max;
constexpr hive_limits(size_t minimum, size_t maximum) noexcept : min(minimum), max(maximum) {}
};
template <class T, class Allocator = allocator<T>>
class hive {
private:
hive_limits current-limits = implementation-defined; // exposition only
public:
// types
using value_type = T;
using allocator_type = Allocator;
using pointer = typename allocator_traits<Allocator>::pointer;
using const_pointer = typename allocator_traits<Allocator>::const_pointer;
using reference = value_type&;
using const_reference = const value_type&;
using size_type = implementation-defined; // see [container.requirements]
using difference_type = implementation-defined; // see [container.requirements]
using iterator = implementation-defined; // see [container.requirements]
using const_iterator = implementation-defined; // see [container.requirements]
using reverse_iterator = std::reverse_iterator<iterator>; // see [container.requirements]
using const_reverse_iterator = std::reverse_iterator<const_iterator>; // see [container.requirements]
constexpr hive() noexcept(noexcept(Allocator())) : hive(Allocator()) { }
explicit hive(const Allocator&) noexcept;
explicit hive(hive_limits block_limits) : hive(block_limits, Allocator()) { }
hive(hive_limits block_limits, const Allocator&);
explicit hive(size_type n, const Allocator& = Allocator());
hive(size_type n, hive_limits block_limits, const Allocator& = Allocator());
hive(size_type n, const T& value, const Allocator& = Allocator());
hive(size_type n, const T& value, hive_limits block_limits, const Allocator& = Allocator());
template<class InputIterator>
hive(InputIterator first, InputIterator last, const Allocator& = Allocator());
template<class InputIterator>
hive(InputIterator first, InputIterator last, hive_limits block_limits, const Allocator& = Allocator());
template<container-compatible-range<T> R>
hive(from_range_t, R&& rg, const Allocator& = Allocator());
template<container-compatible-range<T> R>
hive(from_range_t, R&& rg, hive_limits block_limits, const Allocator& = Allocator());
hive(const hive& x);
hive(hive&&) noexcept;
hive(const hive&, const type_identity_t<Allocator>&);
hive(hive&&, const type_identity_t<Allocator>&);
hive(initializer_list<T> il, const Allocator& = Allocator());
hive(initializer_list<T> il, hive_limits block_limits, const Allocator& = Allocator());
~hive();
hive& operator=(const hive& x);
hive& operator=(hive&& x) noexcept(allocator_traits<Allocator>::propagate_on_container_move_assignment::value || allocator_traits<Allocator>::is_always_equal::value);
hive& operator=(initializer_list<T>);
template<class InputIterator>
void assign(InputIterator first, InputIterator last);
template<container-compatible-range <T> R>
void assign_range(R&& rg);
void assign(size_type n, const T& t);
void assign(initializer_list<T>);
allocator_type get_allocator() const noexcept;
// iterators
iterator begin() noexcept;
const_iterator begin() const noexcept;
iterator end() noexcept;
const_iterator end() const noexcept;
reverse_iterator rbegin() noexcept;
const_reverse_iterator rbegin() const noexcept;
reverse_iterator rend() noexcept;
const_reverse_iterator rend() const noexcept;
const_iterator cbegin() const noexcept;
const_iterator cend() const noexcept;
const_reverse_iterator crbegin() const noexcept;
const_reverse_iterator crend() const noexcept;
// capacity
[[nodiscard]] bool empty() const noexcept;
size_type size() const noexcept;
size_type max_size() const noexcept;
size_type capacity() const noexcept;
void reserve(size_type n);
void shrink_to_fit();
void trim_capacity() noexcept;
void trim_capacity(size_type n) noexcept;
// modifiers
template <class... Args> iterator emplace(Args&&... args);
iterator insert(const T& x);
iterator insert(T&& x);
void insert(size_type n, const T& x);
template<class InputIterator>
void insert(InputIterator first, InputIterator last);
template<container-compatible-range <T> R>
void insert_range(R&& rg);
void insert(initializer_list<T> il);
iterator erase(const_iterator position);
iterator erase(const_iterator first, const_iterator last);
void swap(hive&) noexcept(allocator_traits<Allocator>::propagate_on_container_swap::value || allocator_traits<Allocator>::is_always_equal::value);
void clear() noexcept;
// hive operations
void splice(hive& x);
void splice(hive&& x);
size_type unique();
template<class BinaryPredicate>
size_type unique(BinaryPredicate binary_pred);
constexpr hive_limits block_capacity_limits() const noexcept;
static constexpr hive_limits block_capacity_hard_limits() noexcept;
void reshape(hive_limits block_limits);
iterator get_iterator(const_pointer p) noexcept;
const_iterator get_iterator(const_pointer p) const noexcept;
void sort();
template <class Compare> void sort(Compare comp);
}
template<class InputIterator, class Allocator = allocator<iter-value-type <InputIterator>>
hive(InputIterator, InputIterator, Allocator = Allocator())
-> hive<iter-value-type <InputIterator>, Allocator>;
template<class InputIterator, class Allocator = allocator<iter-value-type <InputIterator>>
hive(InputIterator, InputIterator, hive_limits block_limits, Allocator = Allocator())
-> hive<iter-value-type <InputIterator>, block_limits, Allocator>;
template<ranges::input_range R, class Allocator = allocator<ranges::range_value_t<R>>>
hive(from_range_t, R&&, Allocator = Allocator())
-> hive<ranges::range_value_t<R>, Allocator>;
template<ranges::input_range R, class Allocator = allocator<ranges::range_value_t<R>>>
hive(from_range_t, R&&, hive_limits block_limits, Allocator = Allocator())
-> hive<ranges::range_value_t<R>, block_limits, Allocator>;
}
explicit hive(const Allocator&) noexcept;
hive, using the specified allocator.
hive(hive_limits block_limits, const Allocator&);
hive, using the specified allocator. Initializes current-limits with block_limits.
explicit hive(size_type n, const Allocator& = Allocator());
hive(size_type n, hive_limits block_limits, const Allocator& = Allocator());
T is Cpp17DefaultInsertable into
*this.hive with n default-inserted elements, using
the specified allocator. If the second overload is called, also initializes current-limits with block_limits.n.
hive(size_type n, const T& value, const Allocator& = Allocator());
hive(size_type n, const T& value, hive_limits block_limits, const Allocator& = Allocator());
T is Cpp17CopyInsertable into
*this.hive with n copies of value, using
the specified allocator. If the second overload is called, also initializes current-limits with block_limits.n.
template<class InputIterator>
hive(InputIterator first, InputIterator last, const Allocator& = Allocator());
template<class InputIterator>
hive(InputIterator first, InputIterator last, hive_limits block_limits, const Allocator& = Allocator());hive equal to the range [first, last), using the specified allocator.
If the second overload is called, also initializes current-limits with block_limits.distance(first, last).
template<container-compatible-range<T> R>
hive(from_range_t, R&& rg, const Allocator& = Allocator());
template<container-compatible-range<T> R>
hive(from_range_t, R&& rg, hive_limits block_limits, const Allocator& = Allocator());hive object with the elements of the range rg, using the specified allocator. If the second overload is called, also initializes current-limits with block_limits.ranges::distance(rg).
hive(initializer_list<T> il, const Allocator& = Allocator());
hive(initializer_list<T> il, hive_limits block_limits, const Allocator& = Allocator());
T is Cpp17CopyInsertable into
*this.hive object with the elements of il, using the specified allocator. If the second overload is called, also initializes current-limits with block_limits.il.size().size_type capacity() const noexcept;
hive can hold
without requiring allocation of more element blocks.void reserve(size_type n);
hive of a planned change
in size, so that it can manage the storage allocation accordingly. Does not
cause reallocation of elements. Iterators to elements in *this
remain valid. If n <= capacity() there are no effects.length_error if n >
max_size()numbered_note.capacity() >= n is true.numbered_note) reserve() uses
Allocator::allocate() which can throw an appropriate exception.
void shrink_to_fit();
T is Cpp17MoveInsertable into
*this.shrink_to_fit is a non-binding request to reduce
capacity() to be closer to size().capacity(), but may reduce
capacity(). It may reallocate elements. If
capacity() is already equal to size() there are
no effects. If an exception is thrown other than by the move constructor of
a non-Cpp17CopyInsertable T, the only effects are that
capacity() may be reduced and reallocation may occur.Allocator::allocate() which can throw an appropriate
exception.*this may change. Reallocation invalidates all the references,
pointers, and iterators referring to the elements in the sequence as well
as the past-the-end iterator.void trim_capacity() noexcept;
void trim_capacity(size_type n) noexcept;
capacity() is reduced accordingly. For the second overload,
capacity() will be reduced to no less than n.
*this are invalidated.
template <class... Args>
iterator emplace(Args&&... args);
iterator insert(const T& x);
iterator insert(T&& x);
void insert(size_type n, const T& x);
template<class InputIterator>
void insert(InputIterator first, InputIterator last);
template<container-compatible-range <T> R>
void insert_range(R&& rg);
void insert(initializer_list<T> il);T is called exactly once for each element inserted.iterator erase(const_iterator
position);iterator erase(const_iterator first,
const_iterator last);
*this also
invalidates the past-the-end iterator.T is
the same as the number of elements erased. Additionally if any active
blocks become empty of elements as a result of the function call, at worst
linear in the number of element blocks.void swap(hive& x)
noexcept(allocator_traits<Allocator>::propagate_on_container_swap::value
|| allocator_traits<Allocator>::is_always_equal::value);
capacity() of
*this with that of x.i + n and i
- n, where i is an iterator into the hive
and n is an integer, are the same as those of next(i,
n) and prev(i, n), respectively. For sort,
the definitions and requirements in [alg.sorting] apply.void splice(hive &x);
void splice(hive &&x);
addressof(x) != this is true.
get_allocator() == x.get_allocator() is true.x into *this
and x becomes empty. Pointers and references to the moved
elements of x now refer to those same elements but as members
of *this. Iterators referring to the moved elements shall
continue to refer to their elements, but they now behave as iterators into
*this, not into x.x
plus all element blocks in *this.length_error if any of x's active
blocks are not within the bounds of
this->current-limits.x are not transferred into
*this. Invalidates the past-the-end iterator for both
x and *this.size_type unique();
template<class BinaryPredicate>
size_type unique(BinaryPredicate binary_pred);binary_pred be equal_to< >{} for the
first overload.binary_pred is an equivalence relation.hive, erases all
elements referred to by the iterator i in the range
[begin() + 1, end()) for which binary_pred(*i, *(i -
1)) is true. Invalidates only the iterators and
references to the erased elements.empty() is false, exactly size() -
1 applications of the corresponding predicate, otherwise no
applications of the predicate.constexpr hive_limits block_capacity_limits()
const noexcept;
current-limits.static constexpr hive_limits
block_capacity_hard_limits() noexcept;
hive_limits struct with the min and
max members set to the implementation's hard limits.void reshape(hive_limits
block_limits);
T is Cpp17MoveInsertable into
*this.
block_limits to
current-limits. If any active blocks in
*this are not within the bounds of block_limits,
elements within those active blocks are reallocated to new or existing
element blocks which are within the bounds. Subsequently any element blocks
in *this which are not within the bounds of
block_limits are deallocated. If an exception is thrown other
than by the move constructor of a non-Cpp17CopyInsertable
T, the only effects are that reallocation may occur and
current-limits may change to a value other than
block_limits.*this.
If reallocation occurs, also linear in the number of elements
reallocated.Allocator::allocate() which can throw an appropriate
exception.
capacity(). If
reallocation occurs, the order of the elements in *this may
change. Reallocation invalidates all the references, pointers, and
iterators referring to the elements in the sequence as well as the
past-the-end iterator.iterator get_iterator(const_pointer p)
noexcept;
const_iterator get_iterator(const_pointer p) const noexcept;
p points to an element in
*this.*this.iterator or const_iterator pointing
to the same element as p.void sort();
template <class Compare>
void sort(Compare comp);T is Cpp17MoveInsertable and
Cpp17MoveAssignable into *this. lvalues of type
T are swappable.hive according to the operator
< or the comp function object. If an exception is
thrown, the order of the elements in *this is unspecified.
Iterators and references to elements may be invalidated.N log N comparisons, where N ==
size().numbered_note) sort() uses
Allocator::allocate() which can throw an appropriate exception.
template<class T, class Allocator, class U>
typename hive<T, Allocator>::size_type
erase(hive<T, Allocator>& c, const U& value);return erase_if(c, [&](auto& elem) { return elem == value; });
template<class T, class Allocator, class Predicate>
typename hive<T, Allocator>::size_type
erase_if(hive<T, Allocator>& c, Predicate pred);
auto original_size = c.size();
for (auto i = c.begin(), last = c.end(); i != last; ) {
if (pred(*i)) {
i = c.erase(i);
} else {
++i;
}
}
return original_size - c.size();
Matt would like to thank: Glen Fernandes and Ion Gaztanaga for restructuring
advice, Robert Ramey for documentation advice, various Boost and SG14/LEWG
members for support, critiques and corrections, Baptiste Wicht for teaching me
how to construct decent benchmarks, Jonathan Wakely, Sean Middleditch, Jens
Maurer (very nearly a co-author at this point really), Tim Song, Patrice Roy
and Guy Davidson for standards-compliance advice and critiques, support,
representation at meetings and bug reports, Henry Miller for getting me to
clarify why the free list approach to memory location reuse is the most
appropriate, Ville Voutilainen and Gašper Ažman for help with the
colony/hive rename paper, Ben Craig for his critique of the tech spec, that
ex-Lionhead guy for annoying me enough to force me to implement the original
skipfield pattern, Jon Blow for some initial advice and Mike Acton for some
influence, the community at large for giving me feedback and bug reports on the
reference implementation.
Also Nico Josuttis for doing such a great job in terms of explaining the
general format of the structure to the committee.
Dedicated to Melodie.
Using plf::hive reference implementation.
#include <iostream>
#include <numeric>
#include "plf_hive.h"
int main(int argc, char **argv)
{
plf::hive<int> i_hive;
// Insert 100 ints:
for (int i = 0; i != 100; ++i)
{
i_hive.insert(i);
}
// Erase half of them:
for (plf::hive<int>::iterator it = i_hive.begin(); it != i_hive.end(); ++it)
{
it = i_hive.erase(it);
}
std::cout << "Total: " << std::accumulate(i_hive.begin(), i_hive.end(), 0) << std::endl;
std::cin.get();
return 0;
} #include <iostream>
#include "plf_hive.h"
int main(int argc, char **argv)
{
plf::hive<int> i_hive;
plf::hive<int>::iterator it;
plf::hive<int *> p_hive;
plf::hive<int *>::iterator p_it;
// Insert 100 ints to i_hive and pointers to those ints to p_hive:
for (int i = 0; i != 100; ++i)
{
it = i_hive.insert(i);
p_hive.insert(&(*it));
}
// Erase half of the ints:
for (it = i_hive.begin(); it != i_hive.end(); ++it)
{
it = i_hive.erase(it);
}
// Erase half of the int pointers:
for (p_it = p_hive.begin(); p_it != p_hive.end(); ++p_it)
{
p_it = p_hive.erase(p_it);
}
// Total the remaining ints via the pointer hive (pointers will still be valid even after insertions and erasures):
int total = 0;
for (p_it = p_hive.begin(); p_it != p_hive.end(); ++p_it)
{
total += *(*p_it);
}
std::cout << "Total: " << total << std::endl;
if (total == 2500)
{
std::cout << "Pointers still valid!" << std::endl;
}
std::cin.get();
return 0;
} Benchmark results for plf::colony (performance and majority of code is identical to std::hive reference implementation) under GCC 9.2 on an Intel Xeon E3-1241 (Haswell 2014) are here.
Old benchmark results for an earlier version of colony under MSVC 2015 update 3, on an Intel Xeon E3-1241 (Haswell 2014) are here. There is no commentary for the MSVC results.
Even older benchmark results for an even earlier version of colony under GCC
5.1 on an Intel E8500 (Core2 2008) are here.
This proposal and its reference implementation, and the original reference implementation, have several differences; one is that the original was named 'colony' (as in: a human, ant or bird colony), and that name has been retained for userbase purposes but also for differentiation. Other differences between hive and colony as of the time of writing follow:
Other differences may appear over time.
See the guide to container selection appendix for a more intensive answer to this question, however for a brief overview, it is worthwhile for performance reasons in situations where the order of container elements is not important and:
Under these circumstances a hive will generally out-perform other std:: containers. In addition, because it never invalidates pointer references to container elements (except when the element being pointed to has been previously erased) it may make many programming tasks involving inter-relating structures in an object-oriented or modular environment much faster, and should be considered in those situations.
Some ideal situations to use a hive: cellular/atomic simulation, persistent octtrees/quadtrees, game entities or destructible-objects in a video game, particle physics, anywhere where objects are being created and destroyed continuously. Also, anywhere where a vector of pointers to dynamically-allocated objects or a std::list would typically end up being used in order to preserve pointer stability, but where order is unimportant.
A deque is reasonably dissimilar to a hive - being a double-ended queue, it requires a different internal framework. In addition, being a random-access container, having a growth factor for element blocks in a deque is problematic (though not impossible). deque and hive have no comparable performance characteristics except for insertion (assuming a good deque implementation). Deque erasure performance can vary substantially depending on implementation, but is generally similar to vector erasure performance. A deque invalidates pointers to subsequent container elements when erasing elements, which a hive does not, and guarantees ordered insertion.
Both a slot map and a hive attempt to create a container where there is reasonable insertion/erasure/iteration performance while maintaining stable links from external objects to elements within the container. In the case of hive this is done with pointers/iterators, in the case of a slot map this is done with keys, which are separate to iterators (which do not stay valid post-erasure/insertion in slot maps). Each approach has some advantages, but the hive approach has more, in my view.
If you use a slot map your external object also needs to store a link to the slot map in order to access a element from it's stored key (or a higher-level object accessing the external object needs to store such a link). This prevents effective use of splicing, since in a post-spliced slot map the external object will be referring to an element which is now in another slot map instance. With a hive there is no need for the external object to have knowledge of the hive instance, as pointers are sufficient to access the elements and maintain validity.
One upside of the slot map approach is if you make a duplicate of a slot map + a duplicate of an external object which accesses it's elements via keys, and send these to a secondary thread, little work need be done - all the keys stored in the external object duplicate will work with the copied slot map, all you need to do is update the external object to use the duplicate slot map, instead of the original.
If you wish to do this with a hive, pointers to it's elements in the duplicate external object will of course not point into the duplicate hive, so any external objects you copy to the secondary thread, which you intend to access the hive, will need their pointers to it's elements re-written. The easiest way to do this is by finding the indexes of the elements in the original hive instance via size_type original_index = std::distance(hive.begin(), hive.get_iterator(pointer));, then using external_object.pointers[original_index] = &*(std::next(hive2.begin(), original_index)); to write the new pointer values. Since std::distance/std::next/etc can be overloaded to be very quick for hive, this will likely not take too much time, but it is an inconvenience.
While I haven't done any benchmarks comparing hive performance to a slot map, I have done extensive benchmarks vs a packed array implementation, which is arguably simpler than a slot map, and hive is faster. From the structure of a slot map it's obvious that slot maps are slower for insertion, erasure and for referencing elements within the slot map via external objects. This is because of the intermediary interfaces of the key resolution array and generation counters which need to be accessed and updated. Slot maps are however faster for iteration since all their data is stored contiguously and iteration does not use the keys/counters. In addition the contiguous storage means using a slot map with SIMD is more straight-forward.
Slot maps use more memory due to the keys/counters. Ignoring element block metadata, a hive implementation can use as little as 2 extra bits of metadata per element (current reference implementation is generally between 10 and 16 bits for performance reasons), but a slot map will typically use 128 bits per element (or 64 on a 32-bit system). This will also lower performance due to higher pressure on the cache and the increased numbers of allocations/deallocations.
Unlike a std::vector, a hive can be read from and inserted-into/erased-from at the same time (provided the erased element is not the same as the element being read), however it cannot be iterated over and inserted-into/erased-from to at the same time. If we look at a (non-concurrent implementation of) std::vector's thread-safe matrix to see which basic operations can occur at the same time, it reads as follows (please note push_back() is the same as insertion in this regard due to reallocation when size == capacity):
| std::vector | Insertion | Erasure | Iteration | Read |
| Insertion | No | No | No | No |
| Erasure | No | No | No | No |
| Iteration | No | No | Yes | Yes |
| Read | No | No | Yes | Yes |
In other words, multiple reads can happen simultaneously, but the potential reallocation and pointer/iterator invalidation caused by insertion/push_back and erasure means those operations cannot occur at the same time as anything else. pop_back() is slightly different in that it doesn't cause reallocation, so pop_back()'s and reads can occur at the same time provided you're not reading from the back(). Likewise a swap-and-pop operation can occur at the same time as reading if neither the erased location nor back() is what's being read.
Hive on the other hand does not invalidate pointers/iterators to non-erased elements during insertion and erasure, resulting in the following matrix:
| hive | Insertion | Erasure | Iteration | Read |
| Insertion | No | No | No | Yes |
| Erasure | No | No | No | Mostly* |
| Iteration | No | No | Yes | Yes |
| Read | Yes | Mostly* | Yes | Yes |
* Erasures will not invalidate iterators unless the iterator points to the erased element.
In other words, reads may occur at the same time as insertions and erasures (provided that the element being erased is not the element being read), multiple reads and iterations may occur at the same time, but iterations may not occur at the same time as an erasure or insertion, as either of these may change the state of the skipfield which is being iterated over, if a skipfield is used in the implementation. Note that iterators pointing to end() may be invalidated by insertion.
So, hive could be considered more inherently thread-safe than a (non-concurrent implementation of) std::vector, but still has many areas which require mutexes or atomics to navigate in a multithreaded environment.
Though I am happy to be proven wrong I suspect hives/colonies/bucket arrays are their own abstract data type. Some have suggested its ADT is of type bag, I would somewhat dispute this as it does not have typical bag functionality such as searching based on value (you can use std::find but it's O(n)) and adding this functionality would slow down other performance characteristics. Multisets/bags are also not sortable (by means other than automatically by key value). Hive does not utilize key values, is sortable, and does not provide the sort of functionality frequently associated with a bag (e.g. counting the number of times a specific value occurs).
Two reasons:
++
and -- iterator operations become O(n) in the number of
active blocks, making them non-compliant with the C++ standard. At the
moment they are O(1); in the reference implementation this
constitutes typically one update for both skipfield and element
pointers, two if a skipfield jump takes the iterator beyond the
bounds of the current block and into the next block. But if empty
blocks are allowed, there could be any number of empty blocks between
the current element and the next one with elements in it. Essentially you get the same scenario
as you do when iterating over a boolean skipfield.Future implementations may find better strategies, and it is best not to overly constraint implementation. For the reasons described in the Design Decisions->Specific Functions section on erase(), retaining the current two back blocks has performance and latency benefits. Therefore reserving no active blocks is non-optimal. Meanwhile, reserving All active blocks is bad for performance as many small active blocks will be reserved, which decreases iterative performance due to lower cache locality. If a user wants more fine-grained control over memory retention they may use an allocator.
The user must obtain the block capacity hard limits of the implementation (via block_capacity_hard_limits()) prior to supplying their own limits as part of a constructor or reshape(), so that they do not trigger undefined behavior by supplying limits which are outside of the hard limits. Hence it was perceived by LEWG that there would be no reason for a hive_limits struct to ever be used with non-user-supplied values eg. zero.
There are 'hard' capacity limits, 'default' capacity limits, 'current' limits and user-defined capacity limits. Current limits are whatever the current min/max capacity limits are in a given instance of hive. Default limits are what a hive is instantiated with if user-defined capacity limits are not supplied. Both default limits and user-defined limits are not allowed to go outside of an implementation's hard limits, which represent a fixed upper and lower limit. New element blocks have a implementation-defined growth factor, so will expand up to the current max limit.
While implementations are free to chose their own limits and strategies, in the reference implementation element block sizes start from either the dynamically-defined default minimum size (8 elements, larger if the type stored is small) or an amount defined by the user (with a minimum of 3 elements, as less than 3 elements is pretty much a linked list.
Subsequent block capacities in the reference implementation increase the total capacity of the hive by a factor of 2 (so, 1st block 8 elements, 2nd 8 elements, 3rd 16 elements, 4th 32 elements etcetera) until the current maximum block size is reached. The default maximum block size in the reference implementation is 255 (if the type sizeof is < 10 bytes) or 8192. These values are based on multiple benchmark comparisons between different maximum block capacities, with different sized types. For larger-than-10-byte types the skipfield bitdepth is (at least) 16 so the maximum capacity 'hard' limit would be 65535 elements in that context, for < 10-byte types the skipfield bitdepth is (at least) 8, making the maximum capacity hard limit 255. Larger capacities do not necessarily perform better because, given a randomized erasure pattern, a larger block may statistically retain more erased elements ie. empty space before it runs out of elements entirely and is removed from the sequence, and therefore can create slowdown during iteration due to low locality.
See the summary in paper P2857R0 which goes into this.
Yes if you're careful, no if you're not.
On platforms which support scatter and gather operations via hardware (e.g.
AVX512) you can use hive with SIMD as much as you want, using gather to
load elements from disparate or sequential locations, directly into a SIMD
register, in parallel. Then use scatter to push the post-SIMD-process
values back to their original locations.
In situations where gather and scatter operations are too expensive or which require elements to be contiguous in memory for SIMD processing, it is more complicated. When you have a bunch of erasures in a hive, there's no guarantee that your objects will be contiguous in memory, even though they are sequential during iteration, as there may be erased elements in between them. Some of them may also be in different element blocks to each other. In these situations if you want to use SIMD with hive, you must do the following:
Generally if you want to use SIMD without gather/scatter, it's easier to use a vector or array.
Since this is a container where insertion position is unspecified,
situations such as the following may occur:
hive<int> t = {1, 2, 3, 4, 5}, t2 = {6, 1, 2, 3, 4};
t2.erase(t2.begin());
t2.insert(5);
In this case it is implementation-defined as to whether or not t == t2
because insertion position is not specified, if the == operator is
order-sensitive.
If the == operator is order-insensitive, there is only one reasonable way
to compare the two containers, which is with is_permutation. is_permutation
has a worst-case time complexity of o(n2), which, while in
keeping with how other unordered containers are implemented, was considered
to be out of place for hive, which is a container where performance and
consistent latency are a focus and most operations are O(1) as a result.
While there are order-insensitive comparison operations which can be done
in o(n log n) time, these allocate, which again was considered
inappropriate for a == operator.
In light of this the bulk of SG14/LEWG considered it more appropriate to remove the ==, != and <=> operators entirely, as these were unlikely to be used significantly with hive anyway. This gives the user the option of using is_permutation if they want an order-insensitive comparison, or std::equal if they want an order-sensitive comparison. In either case it removes ambiguity about what kind of operation they are expecting and the time complexity associated with it.
Asides from functions which erase existing elements like clear, erase, ~hive and the = operators, the following may also change ordering: insert/emplace (as position is undefined), reshape, shrink_to_fit, splice.
This was a convenience function to allow programmers to find a hive's current memory usage without using a debugger or profiler, however this was considered out of keeping with current standard practice ie. unordered_map also uses a lot of additional memory but we don't provide such a function. In addition, the context where it would've been useful in realtime (ie. determining whether or not it's worth calling trim_capacity() or shrink_to_fit()), is better approached by comparing size() to capacity().
This was a hint to the implementation to prioritize for lowered memory usage or performance specifically. In other implementations this could've, for example, been used to switch between a jump-counting skipfield and the bitfield+jump-counting approach described in the alternative implementations appendix (reducing memory cost at cost of performance). In the early reference implementation, this told the container to switch between 16-bit and 8-bit skipfield types (smaller bitdepth skipfield types limit the block capacities due to the constraints of the jump-counting skipfield pattern). However, prior to a particular LEWG thread there had not been sufficient benchmarking and memory testing done on this.
When more thorough benchmarking including memory assessments were done, it was found that the vast bulk of unnecessary memory usage came from erased elements in hive when an active block was not yet empty (and therefore freed to the OS or reserved, depending on implementation), rather than the skipfield type. This meant that making block capacities appropriately-sized was more important to performance and cache friendliness than the skipfield type, as - assuming a randomised erasure pattern - smaller blocks were more likely to become empty and therefore be removed from the iterative sequence than larger blocks, thereby improving element contiguousness and iteration performance by skipblocks. But also, reusing erased element memory space in existing element blocks was much faster than having to deallocate/reserve blocks and subsequently allocate or un-reserve new element blocks, so, having too-small element block capacities was also bad.
The only place where the sizeof(skipfield_type) turned out to be more important than block capacities was when using small types such as scalars, where the additional memory use from the skipfield (proportional to the type size) was significant, and so reducing the skipfield_type from 16-bits to 8-bits improved performance even though it made the max block capacities very small (255 elements), due to cache effects.
As a result of all this it was decided to remove the priority parameter and let implementations decide when to switch internal mechanisms, rather than relying on user guesswork; probably a better approach. I think the priority parameter might've been useful for additional compile-time decision processes, such as deciding what type of block retention strategy to use when an active block becomes empty of elements. Also, having a priority tag gave the ability to specify new priority values in future as part of the standard, potentially allowing for big changes without breaking ABI. However, it is also a matter o fcomplexity vs simplicity, and simplicity is worthwhile too.
These are useful for several reasons:
it1 > it2.In the current reference implementation (at time of writing) in the event of needing to allocate a new active block or change a reserved block into an active block, there is an update of active block numbers which may occur if the current back block has a group number == std::numeric_limits<size_type>::max(). The occurence of this event is 1 in every std::numeric_limits<size_type>::max() block allocations/transfers-from-reserved (ie. basically never in the lifetimes of almost all programs). The number of active blocks at this point could be small or large depending on how many blocks have been deallocated in the past.
If a hive were implemented as a vector of pointers to blocks instead, this would also necessitate amortized time complexity as when the vector became full and more blocks were needed, all element block pointers would need to be reallocated to a new memory block.
current-limits to be something other than the original
current-limits and the user-supplied block_limits?If reshaping a hive instance from, for example, a current-limits of min =
6 elements, max = 12 elements, to a supplied user limit of min = 15
elements, max = 255 elements, this basically means none of the original
blocks fit within the new limits. So all elements have to go
into new blocks. A very basic strategy would be to allocate all new active blocks before copying elements, then
deallocating all old active blocks once elements have been copied over. However if there are many active blocks, this could potentially lead to out-of-memory exceptions. So an implementation might choose
to allocate blocks one-at-a-time, copy elements into it, then deallocate each
old block as it becomes empty.
If the latter strategy is pursued we don't necessarily have the old memory
blocks to revert to if an exception is thrown and we're halfway through
copying the elements over. And we wouldn't want to start creating new
element blocks of the old capacity and copy the elements back to them, as
this risks yet more exceptions! The best strategy in this scenario is to keep
all existing blocks, remove duplicate elements if any exist, and change
current-limits to values which accomodate both
the original block capacities and the new block capacities.
Cpp17MoveAssignable is obvious, Cpp17MoveInsertable is to deal with the event that a specific sorting technique wants to take advantage of erased element memory spaces between active elements. For example, for the hive sequence: 4, 3, 5 - where there is an erased element memory space before 4 - the sort technique could simply move-construct the 3 to the erased element memory space instead of swapping with the 4, saving instructions and the creation of a temporary. Also, the sort routine could choose to use erased element memory spaces, if they exist, or empty space at the back of the container, as space to store temporary buffers for swap operations instead of dynamically-allocating buffers - this may be useful both to performance and memory use, if elements are very large.
See paper P2332R0.
The container was originally designed for highly object-oriented situations where you have many elements in different containers linking to many other elements in other containers. This linking can be done with pointers or iterators in hive (insert returns an iterator which can be dereferenced to get a pointer, pointers can be converted into iterators with get_iterator (for use with erase)) and because pointers/iterators stay stable regardless of insertion/erasure to other elements, this usage is unproblematic. You could say the pointer is equivalent to a key in this case but without the overhead. That is the first access pattern, the second is straight iteration over the container. However, the container can have (typically better than O(n)) std::advance/next/prev overloads, so multiple elements can be skipped efficiently.
I'm not really sure how to answer this, as I don't see the resemblance, unless you count maps, vectors etc as being allocators also. The only aspect of it which resembles what an allocator might do, is the memory re-use mechanism. It would be impossible for an allocator to perform a similar function while still allowing the container to iterate over the data linearly in memory, preserving locality, in the manner described in this document.
This is true for many/most AAA game companies who are on the bleeding edge, as well as some of the more hardcore indie developers, but they also do this for vector etc, so they aren't the target audience of std:: for the most part; sub-AAA game companies are more likely to use std::/third party/pre-existing tools. Also, this type of structure crops up in many fields, not just game dev. So the target audience is probably everyone other than people working on bare metal core loops in extreme-high-performance circumstances, but even then, it facilitates communication across fields and companies as to what this type of container is, giving it a standardized name and understanding.
The only analysis done has been around the question of whether it's possible for this specification to fail to allow for a better implementation in future. Bucket arrays have been around since the 1990s at least, there's been no significant innovation in them until now. I've been researching/working on hive since early 2015, and while I can't say that a better implementation might not be possible, I am confident that no change should be necessary to the specification to allow for future implementations. If a change were necessary it would likely be a loosening of the specification rather than a breaking change. This is because of the C++ container requirements and how these constrain implementation.
The requirement of allowing no reallocations upon insertion or erasure, truncates possible implementation strategies significantly. Element blocks have to be independently allocated so that they can be removed from the iterative sequence (when empty) without triggering reallocation of subsequent elements. There's limited numbers of ways to do that and keep track of the element blocks at the same time. Erased element locations must be recorded (for future re-use by insertion) in a way that doesn't create allocations upon erasure, and there's limited numbers of ways to do this also. Multiple consecutive erased elements have to be skipped in O(1) time in order for the iterator to meet the C++ iterator O(1) function requirement, and again there're limits to how many ways you can do that. That covers the three core aspects upon which this specification is based. See the alt implementation appendix for more information.
With splice and unique we can retain the guarantee that pointers to non-erased elements stay valid (sort does not guarantee this for hive), but with merge we cannot, as the function requires an interleaving of elements, which is impossible to accomplish without invalidating pointers, unless the elements are allocated individually. This is not the case in hive, hence including merge may confuse users as to why it doesn't share that same property of valid pointers with std::list. std::sort however is known to invalidate pointers when used with vectors and deques, so sort() as a member function does not necessarily have the association of retaining pointer validity.
This was a choice by LEWG to avoid confusing the user, as insertion position into a hive is implementation-defined. In the case of hive, resizing would not necessarily insert new elements to the back of the container, when the supplied size was larger than the existing size(). New elements could be inserted into erased elements memory locations. This means the initialization of those non-contiguous elements (if they are POD types) cannot be optimized by use of memset, removing the main performance reason to include resize(). The lack of ability to specify the position of insertion removes the "ease of developer use" reason to include resize().
At time of writing constexpr containers are still a new-ish thing and some of the kinks of usage may yet have to be worked out. Early compiler support was not good but this has improved steadily over time. I wasn't happy with having to label each and every function as constexpr, but there seem to be movements toward labeling classes as a whole as constexpr, so if that comes through it will remove that problem. Having said that, there are a couple of things to consider when designed a constexpr hive. One is that in the reference implementation there is extensive use of reinterpret_cast'ing pointers, mainly for two areas:
As reinterpret_cast is not allowed at compile time, 1 could be worked around by creating a union between the element type and the free list struct/pair. 2 would not be possible at compile time, and the element block and skipfield blocks would have to be allocated separately. So it is possible, though it could be hard work, and may decrease runtime performance.
Constexpr containers do not allow non-literal member variables, and in the reference implementation the begin() and end() iterators are stored as member variables and also function as records of the first and last active blocks in the sequence. This much can be worked around by breaking the iterators apart into their individual pointers, then reconstructing them on the fly whenever begin()/end()/etc are called.
For the moment I am happier for std::array and std::vector to be the "canaries in the coalmine" here.
Yes. zLib license is compatible with both GPL3 and Apache licenses (libc++/MS-STL). zLib is a more permissive license than all of these, only requiring the following:
This software is provided 'as-is', without any express or implied
warranty. In no event will the authors be held liable for any damages
arising from the use of this software.
Permission is granted to anyone to use this software for any
purpose, including commercial applications, and to alter it and
redistribute it freely, subject to the following restrictions:
The origin of this software must not be misrepresented; you
must not claim that you wrote the original software. If you use this
software in a product, an acknowledgment in the product documentation
would be appreciated but is not required.Altered source versions must be plainly marked as such, and
must not be misrepresented as being the original software.This notice may not be removed or altered from any source
distribution.Please note that "product" in this instance doesn't mean 'source code', as in a library, but a program or executable. This is made clear by line 3 which clearly differentiates source distributions from products.
Representatives from libc++, libstdc++ and MS-STL have stated they will likely either use the reference or use it as a starting point, and that licensing is unproblematic (with the exception of libc++ who stated they would need to run it past LLVM legal reps). However if in any case licensing becomes problematic as the sole author of the reference implementation I am in a position to grant use of the code under other licenses as needed.
It doesn't. Detecting these cases is the end user's responsibility, as it is in deque or vector when elements are erased. In the case of hive I would recommend the use of either a unique ID within the element itself. The end user can then build their own "handle" wrapper around a pointer or iterator which stores a copy of this ID, then compares it against the element itself upon accessing it to see if it's the same.
In terms of guarantees that an element has not been replaced via hive usage, replacement may occur if:
An allocator can only decrease the number of allocation calls to the OS. While it might allocate one small block contiguous to another in the order of the sequence, it also might not (and likely won't), which decreases iteration speed. Further, there is a certain amount of metadata necessary for each block (regardless of implementation), which needs to be updated etc when erasures/insertions happen. Hence, by having more blocks than you need, you also increase memory overhead. There is also procedural overhead associated with each block, in terms of many of the operations like splice, reshape and reserve, where the more blocks you have, the more operations you incur (though the cost is typically very low).
Places to start: read the first paragraph of the introduction to this
paper, then the Design Decisions section, then the constraints and alt implementation appendices.
Most of the specificity comes from the type of container and the C++
standard's specifications. In terms of this type of container, this paper
represents to the best of my knowledge the widest scope of implementation
while still fulfilling the core invariants of the container, maintaining
reasonable performance, and satisfying the C++ standard requirements.
There is also a risk of underspecification. The (at time of writing) MS STL version of deque allocates blocks in a fixed size of 16 bytes so any element type above 8 bytes makes it a linked list - which it is allowed to do by the standard, which does not allow the user to specify block capacities. There are advantages to being more specific when you get to something more complex than an array because it encourages good implementation practice. As a result we attempt to reach a balance between under/over-specification.
current-limits between hives?hive<int> h(hive_limits(10,50));
h = other_hive;
Likewise if the user wants to specify new capacity limits when moving
from another hive, they could:
hive<int> h(std::move(other_hive));
h.reshape(10, 50);
Here are some more specific requirements with regards to game engines, verified by game developers within SG14:
std::vector in its default state does not meet these requirements due to:
Game developers therefore tend to either develop custom solutions for each scenario or implement workarounds for vector. The most common workarounds are most likely the following or derivatives thereof:
Hive brings a more generic solution to these contexts with better performance according to my benchmarks.
"I'm the lead of the Editors team at Creative Assembly, where we make tools for the Total War series of games. The last game we released was Three Kingdoms, currently doing quite well on Steam. The main tool that I work on is the map creation editor, kind of our equivalent of Unreal Editor, so it's a big tool in terms of code size and complexity.
The way we are storing and rendering entities in the tool currently is very inefficient: essentially we have a quadtree which stores pointers to the entities, we query that quadtree to get a list of pointers to entities that are in the frustum, then we iterate through that list calling a virtual draw() function on each entity. Each part of that process is very cache-unfriendly: the quadtree itself is a cache-unfriendly structure, with nodes allocated on the heap, and the entities themselves are all over the place in memory, with a virtual function call on top.
So, I have made a new container class in which to store the renderable versions of the entities, and this class has a bunch of colonies inside, one for each type of 'renderable'. On top of this, instead of a quadtree, I now have a virtual quadtree. So each renderable contains the index of the quadtree node that it lives inside. Then, instead of asking the quadtree what entities are in the frustum, I ask the virtual quadtree for a node mask of the nodes what are in the frustum, which is just a bit mask. So when rendering, I iterate through all the renderables and just test the relevant bit of the node mask to see if the renderable is in the frustum. (Or more accurately, to see if the renderable has the potential to be in the frustum.) Nice and cache friendly.
When one adds an entity to the container, it returns a handle, which is just a pointer to the object inside one of the colonies returned as a std::uintptr_t. So I need this to remain valid until the object is removed, which is the other reason to use a colony."
"I implemented a standalone open source project for the thread liveness monitor: https://github.com/shuvalov-mdb/thread-liveness-monitor. Also, I've made a video demo of the project: https://youtu.be/uz3uENpjRfA
The benchmarks are in the doc, and as expected the plf::colony was extremely fast. I do not think it's possible to replace it with any standard container without significant performance loss. Hopefully, this version will be very close to what we will put into the MongoDB codebase when this project is scheduled."
"I'm using it as backing storage for a volumetric data structure (like openvdb). Its sparse so each tile is a 512^3 array of float voxels.
I thought that having colony will allow me to merge multiple grids together
more efficiently as we can just splice the tiles and not copy or reallocate
where the tiles dont overlap. Also adding and removing tiles will be fast. Its
kind of like using an arena allocator or memory pool without having to actually
write one."
Note: this is a private project Daniel is working on, not one for Weta
Digital.
"Internally we use it as a slab allocator for objects with very different lifetime durations where we want aggressive hot memory reuse. It lets us ensure the algorithms are correct after the fact by being able to iterate over the container and verify what's alive.
It's a great single-type memory pool, basically, and it allows iteration for debugging purposes :)
Where it falls slightly short of expectation is having to iterate/delete/insert under a lock for multithreaded operation - for those usecases we had to do something different and lock-free, but for single-threaded applications it's amazing."
Guides and flowcharts I've seen online have either been performance-agnostic or incorrect. This is not a perfect guide, nor is it designed to suit all participants, but it should be largely correct in terms of it's focus. Note, this guide does not cover:
These are broad strokes and should be treated as such. Specific situations with specific processors and specific access patterns may yield different results. There may be bugs or missing information. The strong insistence on arrays/vectors where-possible is for code simplicity, ease of debugging, and performance via cache locality. For the sake of brevity I am purposefully avoiding any discussion of the virtues/problems of C-style arrays vs std::array or vector here. The relevance of all assumptions are subject to architecture. The benchmarks this guide is based upon are available here, here. Some of the map/set data is based on google's abseil library documentation.
a = yes, b = no
0. Is the number of elements you're dealing with a fixed amount? 0a. If so, is all you're doing either pointing to and/or iterating over elements? 0aa. If so, use an array (either static or dynamically-allocated). 0ab. If not, can you change your data layout or processing strategy so that pointing to and/or iterating over elements would be all you're doing? 0aba. If so, do that and goto 0aa. 0abb. If not, goto 1. 0b. If not, is all you're doing inserting-to/erasing-from the back of the container and pointing to elements and/or iterating? 0ba. If so, do you know the largest possible maximum capacity you will ever have for this container, and is the lowest possible maximum capacity not too far away from that? 0baa. If so, use vector and reserve() the highest possible maximum capacity. Or use boost::static_vector for small amounts which can be initialized on the stack. 0bab. If not, use a vector and reserve() either the lowest possible, or most common, maximum capacity. Or boost::static_vector. 0bb. If not, can you change your data layout or processing strategy so that back insertion/erasure and pointing to elements and/or iterating would be all you're doing? 0bba. If so, do that and goto 0ba. 0bbb. If not, goto 1. 1. Is the use of the container stack-like, queue-like or ring-like? 1a. If stack-like, use plf::stack, if queue-like, use plf::queue (both are faster and configurable in terms of memory block sizes). If ring-like, use ring_span or ring_span lite. 1b. If not, goto 2. 2. Does each element need to be accessible via an identifier ie. key? ie. is the data associative. 2a. If so, is the number of elements small and the type sizeof not large? 2aa. If so, is the value of an element also the key? 2aaa. If so, just make an array or vector of elements, and sequentially-scan to lookup elements. Benchmark vs absl:: sets below. 2aab. If not, make a vector or array of key/element structs, and sequentially-scan to lookup elements based on the key. Benchmark vs absl:: maps below. 2ab. If not, do the elements need to have an order? 2aba. If so, is the value of the element also the key? 2abaa. If so, can multiple keys have the same value? 2abaaa. If so, use absl::btree_multiset. 2abaab. If not, use absl::btree_set. 2abab. If not, can multiple keys have the same value? 2ababa. If so, use absl::btree_multimap. 2ababb. If not, use absl::btree_map. 2abb. If no order needed, is the value of the element also the key? 2abba. If so, can multiple keys have the same value? 2abbaa. If so, use std::unordered_multiset or absl::btree_multiset. 2abbab. If not, is pointer stability to elements necessary? 2abbaba. If so, use absl::node_hash_set. 2abbabb. If not, use absl::flat_hash_set. 2abbb. If not, can multiple keys have the same value? 2abbba. If so, use std::unordered_multimap or absl::btree_multimap. 2abbbb. If not, is on-the-fly insertion and erasure common in your use case, as opposed to mostly lookups? 2abbbba. If so, use robin-map. 2abbbbb. If not, is pointer stability to elements necessary? 2abbbbba. If so, use absl::flat_hash_map<Key, std::unique_ptr<Value>>. Use absl::node_hash_map if pointer stability to keys is also necessary. 2abbbbbb. If not, use absl::flat_hash_map. 2b. If not, goto 3. Note: if iteration over the associative container is frequent rather than rare, try the std:: equivalents to the absl:: containers or tsl::sparse_map. Also take a look at this page of benchmark conclusions for more definitive comparisons across more use-cases and hash map implementations. 3. Are stable pointers/iterators/references to elements which remain valid after non-back insertion/erasure required, and/or is there a need to sort non-movable/copyable elements? 3a. If so, is the order of elements important and/or is there a need to sort non-movable/copyable elements? 3aa. If so, will this container often be accessed and modified by multiple threads simultaneously? 3aaa. If so, use forward_list (for its lowered side-effects when erasing and inserting). 3aab. If not, do you require range-based splicing between two or more containers (as opposed to splicing of entire containers, or splicing elements to different locations within the same container)? 3aaba. If so, use std::list. 3aabb. If not, use plf::list. 3ab. If not, use hive. 3b. If not, goto 4. 4. Is the order of elements important? 4a. If so, are you almost entirely inserting/erasing to/from the back of the container? 4aa. If so, use vector, with reserve() if the maximum capacity is known in advance. 4ab. If not, are you mostly inserting/erasing to/from the front of the container? 4aba. If so, use deque. 4abb. If not, is insertion/erasure to/from the middle of the container frequent when compared to iteration or back erasure/insertion? 4abba. If so, is it mostly erasures rather than insertions, and can the processing of multiple erasures be delayed until a later point in processing, eg. the end of a frame in a video game? 4abbaa. If so, try the vector erase_if pairing approach listed at the bottom of this guide, and benchmark against plf::list to see which one performs best. Use deque with the erase_if pairing if the number of elements is very large. 4abbab. If not, goto 3aa. 4abbb. If not, are elements large or is there a very large number of elements? 4abbba. If so, benchmark vector against plf::list, or if there is a very large number of elements benchmark deque against plf::list. 4abbbb. If not, do you often need to insert/erase to/from the front of the container? 4abbbba. If so, use deque. 4abbbbb. If not, use vector. 4b. If not, goto 5. 5. Is non-back erasure frequent compared to iteration? 5a. If so, is the non-back erasure always at the front of the container? 5aa. If so, use deque. 5ab. If not, is the type large, non-trivially copyable/movable or non-copyable/movable? 5aba. If so, use hive. 5abb. If not, is the number of elements very large? 5abba. If so, use a deque with a swap-and-pop approach (to save memory vs vector - assumes standard deque implementation of fixed block sizes) ie. when erasing, swap the element you wish to erase with the back element, then pop_back(). Benchmark vs hive. 5abbb. If not, use a vector with a swap-and-pop approach and benchmark vs hive. 5b. If not, goto 6. 6. Can non-back erasures be delayed until a later point in processing eg. the end of a video game frame? 6a. If so, is the type large or is the number of elements large? 6aa. If so, use hive. 6ab. If not, is consistent latency more important than lower average latency? 6aba. If so, use hive. 6abb. If not, try the erase_if pairing approach listed below with vector, or with deque if the number of elements is large. Benchmark this approach against hive to see which performs best. 6b. If not, use hive. Vector erase_if pairing approach: Try pairing the type with a boolean, in a vector, then marking this boolean for erasure during processing, and then use erase_if with the boolean to remove multiple elements at once at the designated later point in processing. Alternatively if there is a condition in the element itself which identifies it as needing to be erased, try using this directly with erase_if and skip the boolean pairing. If the maximum number of elements is known in advance, use vector with reserve().
This is a summary of information already contained within P0447.
So in order to serve the requirements of high performance, stable memory locations, and the C++ standard, a standard library implementation of this type of container is quite constrained as to how it can be specified. Ways of meeting those constraints which deviate from reference implementation are detailed in the alt implementations appendix.
In addition to the stuff below I have written a supporting paper which attempts to assess prevalence of this type of container within the programming industry - with the results being about 61% of respondents using something like it (see P3011).
Sean Middleditch talks about 'arrays with holes' on his old blog, which is similar but using id lookup instead of pointers. There is some code: link
Jonathan Blow talks about bucket arrays here (note, he says "I call it a bucket array" which might connote that it's his concept depending on your interpretation, but it's just an indication that there are many names for this sort of thing): link
A github example (no iteration, lookup-only based on entity id): link
This guy describes free-listing and holes in 'deletion strategies': link
Similar concept, static array with 64-bit integer as bit-field for skipping: link
Going over old colony emails I found someone whose company had implemented something like the above but with atomic 64-bit integers for boolean (bitfield) skipfields and multi-blocks for multithreaded use.
I initially thought while I was developing this that it was a newish concept, but particularly after doing the cppcon talk, more people kept coming forward saying, yes, we do this, but with X specific difference.
Pool allocators etc are often constructed similarly to hives, at least in terms of using free lists and multi memory blocks. However they are not useful if you have large amounts of elements which require bulk processing for repeated timeframes, because an allocator doesn't provide iteration, and manually iterating via say, a container of pointers to objects in a pool has the same performance and memory-use issues as linked lists.
See the Design Decisions section for a revision on these and how the reference implementation applies them, and below for the alternatives.
It is possible to implement a hive via a vector of pointers to blocks+metadata. Some of the metadata could be stored with the pointers in the vector. More analysis of this approach is described in the section below this one, A full implementation guide using the vector-of-pointers-to-blocks approach.
The low-complexity jump-counting pattern used in the reference implementation has a lot of similarities to the high complexity jump-counting pattern, which was a pattern previously used by the original reference implementation. Using the high-complexity pattern is an alternative, though the skipfield update time complexity guarantees for insertion/erasure with that pattern are at-worst O(n) in the number of elements in the block. In practice the majority of those updates constitute a single memcpy operation which may resolve to a much smaller number of operations at the hardware level. But it is still slightly slower than the low-complexity jump-counting pattern (around 1-2% in my benchmarking).
A pure boolean skipfield is not usable because it makes iteration time complexity at-worst O(n - 2) in the summed capacity of two blocks (ie. a non-erased element at the beginning of one block, with no subsequent non-erased elements till the end of the next block). This can result in thousands of branching statements & skipfield reads for a single ++ operation in the case of many consecutive erased elements. In the high-performance fields for which this container was initially designed, this brings with it unacceptably unpredictable latency.
However another strategy combining a low-complexity jump-counting pattern and a boolean skipfield, which saves memory at the expense of computational efficiency, is possible while preserving O(1) iterator operations. There is a simpler version of this, and a more complex version - both of which have some advantages.
This approach introduces 3 additional sets of operations per iteration via (1) branching operations when checking the bitfield, (2) bitmasking + bitshift to read the bits and (3) additional reads (from the erased element memory space). But it does reduce the memory overhead of the skipfield to 1 bit per-element. Unfortunately this also means the type has to be wide enough to fit both free list indexes and the jump-counting data - which means, assuming a doubly-linked free list, the type must be 32-bits or greater (assuming max block capacities of 255 elements, meaning the free list indexes can be 8-bit each), otherwise it's storage will need to be artificially widened to 32 bits. There is a way around this though:
++ iteration becomes:
-- iteration becomes:
This approach involves a greater number of operations than the simple variant, but means that for a 16-bit type and max block capacities of 255 elements (meaning the free list indexes can be 8-bit), the type's storage will not need to be artificially widened in order to store both the doubly-linked free list and jump-counting data.
One cannot use a stack of pointers (or similar) to erased elements for this mechanism, as early versions of the reference implementation did, because this can create allocations during erasure, which violates the exception guarantees of erase() in the standard.
If a global (ie. not per-element-block) free list were used, pointers would be necessary instead of indexes, as finding the location of an erased element based on a (global) index would be O(n) in the number of active blocks (counting each block's capacity as we went). This would increase the minimum bitdepth necessary for the hive element type to sizeof(pointer) * 2. A global free list would also decrease cache locality when traversing the free list by jumping between element blocks. Lastly, when a block was removed from the active blocks upon becoming empty, it would force an O(n) traversal of the free-list to find all erased elements (or skipblocks) within that particular block in order to remove them from the free list. Hence a global free list is unacceptable for both performance and latency reasons.
Previous versions of the reference implementation used a singly-linked free list of erased elements instead of a doubly-linked free list of skipblocks. This is possible with the high complexity jump-counting pattern, but not using the low complexity jump-counting pattern, as the latter cannot calculate the location of the start node of a skipblock from the value of a non-start node, but the high complexity variant can (see both of the jump-counting papers listed earlier for more details). But using free-lists of skipblocks is more efficient as it requires fewer free list nodes. In addition, re-using only the start or end nodes of a skipblock is faster because it never splits a skipblock into two skipblocks.
An example of why a doubly-linked free list is necessary for the low complexity jump-counting pattern, is erasing an element which happens to be between two skipblocks. In this case two skipblocks must be combined into one skipblock, and the previous secondary skipblock must be removed from that block's free list. If the free list is singly-linked, the hive must do a linear search through the free list, starting from the free list head, in order to find the skipblock prior to the secondary skipblock mentioned, to update that free list node's "next" index link. This is at worst O(n) in the number of skipblocks within that block. However if a doubly-linked free list is used, that previous skipblock is linked to from the entry in the skipblock we have to remove, making the free list update constant-time.
Likewise when an erasure occurs just before the front of a skipblock (where the free-list data is stored), expanding the skipblock, the same scenario applies; for a singly-linked free list, one has to traverse the whole free list starting from the free list head, in order to find that skipblock's 'previous' free list node in order to update the previous node's 'next' link to point to the new start location of the changed skipblock. If the free list is doubly-linked we don't have to.
If the high-complexity jump-counting pattern is used, then we can calculate the start of a skipblock from the value of the erased skipfield node; and from the start nodes value we know the length of the skipblock. This means we can alter skipblocks using the information given to us by any node in the skipblock, not just the back/front nodes. Which in turn means we can make a free list from individual erased elements rather than skipblocks. And this in turn means there is no need to combine or update previously-existing free list entries in the examples above, and we can simply use a singly-linked free list instead of a doubly-linked one.
So far I have largely been talking about how to keep track of erasures within element blocks, not about which blocks have erasures in them. In the reference implementation the latter is achieved by keeping an intrusive linked list of the groups whose blocks contained erasures, as mentioned previously. This increases group metadata memory usage by two pointers. Alternative methods include:
size_type per active block.In the reference implementation we do not accommodate 1-byte types without artificially widening the storage the type uses to be sizeof(skipfield_type) * 2 ie. 2 bytes. This is in order to accomodate the doubly-linked free list of skipblocks, which is expressed in pairs of prev/next indexes written to the erased element's memory location. Those indexes have to be able to address the whole of the specific element block, which means they have to be the same size as skipfield_type.
If an implementation wished to create an overload for 1-byte types such that there was no artificial widening of the element storage and the resultant wasted memory, there are 6 valid approaches I can see.
In this approach we reduce the skipfield bit-depth to 4-bits which in turn reduces the capacities of element blocks to 16 elements. We can do this via a bit-field. We then continue business-as-usual and store our free list node data in the erased element memory space. Blocks are 15-elements wide rather than 16 elements as we need to reserve the value of numeric_limits<skipfield_type>::max() as described above.
Here we take the bitfield + jump-counting skipfield (complex variant) approach. Again, since our block size is 15 elements, jump-counting data can be stored using 4-bit integers. So the free list's prev and next indexes can be stored within the memory space of a single 1-byte erased element, while the jump-counting data is stored in the memory space of both the second and last erased elements in the skipblock.
Here, instead of artificially widening type storage so that we can store 2 bytes of free list data in it, we create a secondary 'next' field (1-byte array) to store the 'next' index of our free list, while the 'prev' index is stored in the erased element's memory space. We then follow the bitfield + jump-counting skipfield (complex variant) approach, storing 8-bit jump-counting data in the memory space of both the second and last erased elements in the skipblock.
Same as the approach above, but instead of having a separate nextfield, we reduce it to 7 bits and combine it with the bitfield to make a singular 8-bit array. 7 bits reduces the max capacity of the element blocks.
Here we substitute the low-complexity jump-counting skipfield for the high-complexity variant, which is at worst O(n) in the number of skipfield nodes in a given block for insertion and erasure, so would require widening of their time complexity. However, our block size is at most 255 elements (with 255 corresponding skipfield nodes) which limits the number of operations. The high-complexity pattern allows us to have a singly-linked free list of erased elements instead of skipblocks for the reasons described earlier. So we can store our 8-bit 'next' value in the erased-element memory space without having to widen the type bitdepth.
Here we take a bitfield + jump-counting skipfield (simple variant) approach and use it with a 4-bit high-complexity jump-counting skipfield. We can store both the jump-counting data + the free list 'next' value in the erased element memory space (since both are 4-bits). Since the block size is fixed at 15 elements, the high-complexity jump-counting approach is effectively O(1).
However if we look at the memory cost of each of these approaches, only two are adequate. Assuming we take a 'vector-of-pointers' approach to implementation + a jump-counting skipfield of blocks-with-erasures (as described in the summary at the start of this appendix) + doing a few other things like allocating the element block and skipfield block in one allocation, and using the offset in capacity from the start of the element block to find the skipfield block (instead of storing a pointer to the skipfield block), we can reduce the per-block metadata down to around 40 bytes. Taking each of the approaches listed above as well as the reference implementation's approach, for 253 elements we would end up with the per-element memory cost being (not including unused skipfield/element block memory space):
Metadata cost: 17 * 40 bytes
Skipfield cost: 253 * 4 bits (.5 bytes)
Additional memory cost per element: 3.19 bytes.
Metadata cost: 17 * 40 bytes
Skipfield cost: 253 * 1 bits (.125 bytes)
Additional memory cost per element: 2.81 bytes.
Metadata cost: 1 * 40 bytes
Nextfield cost: 253 * 1 byte
Skipfield cost: 253 * 1 bits (.125 bytes)
Additional memory cost per element: 1.28 bytes.
Metadata cost: 2 * 40 bytes
Combined skipfield/nextfield cost: 253 * 1 bytes
Additional memory cost per element: 1.32 bytes.
Metadata cost: 1 * 40 bytes
Skipfield cost: 253 * 1 bytes
Additional memory cost per element: 1.16 bytes.
Metadata cost: 17 * 40 bytes
Skipfield cost: 253 * 1 bit (.125 bytes)
Additional memory cost per element: 2.97 bytes.
Metadata cost: 1 * 40 bytes
Widening cost: 253 * 1 bytes
Skipfield cost: 253 * 1 bytes
Additional memory cost per element: 2.16 bytes.
Clearly the third, fourth and fifth approaches are the only viable ones, if memory waste is a concern. They also allow allocating larger numbers of elements contiguously and reduce the number of allocations/deallocations, which improves insert/erase/iteration performance compared to other non-reference approaches. Since only the third and fourth don't require changing the API, they would be the better approaches, between those two the third has better cache locality due to larger element blocks, and also less memory waste so that's the preferred one.
I will give the summary first, then show in detail, how we get there and why some approaches aren't possible. When I talk about vectors here I'm not really talking about std::vector, more likely a custom implementation.
Like in the reference implementation, there are structs (referred to herein as 'groups') containing both an element array + skipfield array + array metadata such as size, capacity etc. Each group has it's own erased-element free list just like the reference implementation.
The hive contains a vector of pointers to groups (referred to herein as a 'group-vector'). The group-vector contains 2 extra pointers, one at the front of the active group pointers and one at the back of the active group pointers, each of which has it's own location in memory as it's value (these are referred to herein as the front and back pointers).
Each allocated group also contains a reverse-lookup pointer in it's metadata which points back to the pointer pointing at it in the group-vector. While this is used in other operations it is also used by iterator comparison operators to determine whether the group that iterator1 is pointing to is later than the group that iterator2 is pointer to, in the iterative sequence.
An iterator maintains a pointer to the group, the current element and the current skipfield location (or just an index into both the element and skipfield arrays). When it needs to transition from the end or beginning of the element array to the next or previous group, it takes the value of the reverse-lookup pointer in the current group's metadata and increments or decrements it respectively, then dereferences the new value to find the next/previous group's memory location.
If the value of the memory location pointed to is nullptr, it
increments/decrements again till it finds a non-nullptr pointer -
this is the next block. If the value of the memory location pointed to is equal
to the memory location, the iterator knows it has reached the front or back
pointer in the vector, depending on whether it was decrementing or incrementing
respectively. This is the only purpose of the front and back pointers, to inform the iterator of boundaries (see later for more details).
When a group becomes empty of non-erased elements, it is either deallocated
or retained for future insertions by copying it's pointer in the group-vector
to an area past the back pointer, depending on implementation. Either way it's
original pointer location in the group-vector is nullptr'ed.
There is a hive member counter which counts the number of
nullptr'ed pointers. If it reaches a implementation-specific
threshold, a erase_if operation is called on the vector, removing all
nullptr pointers and consolidating the rest. Subsequently (or as
part of the erase_if operation) the groups whose pointers have been relocated
have their reverse-lookup pointer updated. The threshold prevents (a) iterator
++/-- functions straying too far from being O(1) amortized in terms of number of operations and
(b) too many erase_if operations occurring.
Likewise for any splice operation, when source groups become part of the destination, the destination group-vector gets pointers to those groups added, and the reverse-lookup pointers in those groups get updated. All reverse-lookup pointers get updated when the vector expands and the pointers are reallocated.
To keep track of groups which currently have erased-element locations ready to be re-used by insert, we can either keep the reference implementation's intrusive-list-of-groups-with-erasures approach, or we can remove that metadata from the group and instead have a secondary vector of size_type with the same capacity as the group-vector, containing a jump-counting skipfield.
In that skipfield we maintain a record of runs of groups which do Not currently have erased element locations available for reuse, so that if there are any such groups available, a single iteration into this skipfield will take us to the index corresponding to that group in the group-vector. And if there are no such groups available, that same iteration will take us to the end of the skipfield. This approach replaces 2 pointers of metadata per-group with one size_type.
If insertion determines that there are no groups with erasures available, it can
(depending on implementation) either check a hive member counter which counts
the number of nullptr'ed pointers, and if it's not zero,
linear-scan the group-vector to find any nullptr locations and
reuse those to point to a new group - or it could just move the back pointer
forward by 1 and reuse that location to point to a new group (relying on the
occasional erase_if operations to clean up the nullptr pointer
locations instead, and running erase_if itself only if the vector has reached
capacity). If the implementation has retained a pointer to an empty group past
the back pointer (a group made empty by erasures) it could reuse that at this
point.
The simplest idea I had for the alternative (non-reference-implementation) approach was, a vector of pointers to allocated element blocks. In terms of how iteration works, the iterator holds a pointer to the vector-of-pointers (the structure, not the vector's internal array) and an index into the vector-of-pointer's array, as well as a pointer/index to the current element. The hive itself would also store a pointer to the vector structure, allocating it dynamically, which makes swapping/moving non-problematic in terms of keeping valid iterators (if the hive stores the vector as a member, the iterator pointers to the vectors get invalidated on swap/move).
When the end of a block is reached by the iterator, if it hasn't hit end() you add 1 to the vector-of-pointers index in the iterator and continue on to the next block. Since the iterator uses indexes, reallocation of the vector array upon expansion of the vector-of-pointers doesn't become a problem. However it is a problem when a block prior to the current block that the iterator is pointing at, becomes empty of elements and has to be removed from the iterative sequence. If the pointer-to-that-block gets erased from the vector-of-pointers, that will cause subsequent pointers to be relocated backward by one, which in turn will make iterators pointing to elements after that block invalid (because the relocation invalidates the stored block indexes in the iterators).
Substituting a swap-and-pop between the erasable pointer and the back pointer of the vector-of-pointers, instead of erasing/relocating, doesn't solve this problem, as this produces unintuitive iteration results when an iterator lies between the back block and the block being erased (suddenly there is a bunch of elements behind it instead of in front, so forward iteration will miss those), and it also invalidates iterators pointing to elements in the (previously) back block.
So at this point we only have two valid approaches, A & B.
Here we have to think it terms of what's efficient, not what necessarily
lowers time complexity requirements. Basically instead of erasing pointers to
the erased blocks from the vector, we mark them as nullptr and the
iterator, when it passes to the next block, skips over the nullptr
pointers. This is the opposite of what we try to do with the current approach
in the reference implementation (remove blocks from the iterative
linked-list-of-blocks sequence) because with the current approach, those blocks
represent a latency issue via following pointers to destinations which may not
be within the cache. With a vector approach however, it makes no difference to
latency because the next pointer in the vector chunk already exists in the
cache in, at a guess, 99% of cases. You could, potentially, get a bad result
when using a CPU with poor branch-prediction-recovery performance like core2's
(because this approach introduces a branching loop), when you have a
close-to-50/50 random distribution of nullptr's and actual
pointers to blocks. But since blocks are generally going to be many factors
fewer than elements within those blocks, this is not likely to be a major
performance hit like a boolean skipfield over elements would be, even in that
case.
In terms of re-using those nullptr pointers, we can't do a
free-list of pointers because then during iteration we would have no idea which
pointer was a pointer to a block and which a pointer to another free-list item
- so instead we simply have a size_type counter in the hive metadata which
counts the number of erased pointers currently in the vector-of-pointers. When
we reach the capacity of existing element blocks and need to create a new block
upon insert, we check the counter - if it's not zero (ie. time to create new a
block pointer at the back of the vector), scan manually along the
vector-of-pointers until you hit a nullptr and re-use that (same
logic as above as to why this isn't a latency/performance issue) and decrement
the 'erased pointer' counter.
Since insertion location is unspecified for hive, inserting a block randomly into the middle of the iterative sequence causes no fundamental issues, is the same as re-using an erased element location during insertion.
If one is concerned about strict time complexity, and less concerned about real world effects of that time complexity, you can basically have a jump-counting skipfield for the vector-of-pointers (secondary vector of size_type with a low-complexity jump-counting skipfield).
This means (a) iterators can skip over pointers to erased blocks in O(1) time and (b) the memory locations of the pointers to erased blocks can be used to form a free list of reusable pointers. So this eliminates both of the non-O(1) aspects of Approach A, though whether or not this is faster in-practice comes down to actual benchmarking.
I've left out block metadata (size, capacity, erased element free list head, etc) in the descriptions above to simplify explanation, but for approach A we would probably want block metadata as part of a struct which the vector-of-pointers is pointing to (struct contains the element block too), so that the non-O(1) linear scans over the vector-of-pointers are as fast as possible.
For approach B we would probably want the vector-of-pointers to actually be a vector-of-struct-metadata, with the pointer to the element block being one of the pieces of metadata. We could also do a 'struct of arrays' approach instead, depending on the performance result.
Both approaches eliminate the need for the 'block number' piece of metadata since we get that from the vector-of-pointers for free. They also eliminate the need for prev-block/next-block pointers, though this is offset by the need for the vector of pointers in approach A and for approach B the secondary skipfield - but still a reduction of 2 pointers to 1 pointer/size_type.
The intrusive-list-of-blocks-with-element-erasures from the reference
implementation could in this approach be replaced with a low-complexity jump-counting skipfield (an additional vector of size_type) which,
instead of denoting runs of erased blocks, denotes runs of blocks with no
prior element erasures (this would include erased blocks, since these are not usable for insert).
If there were no prior erasures, iterating over this skipfield would jump directly to the end of the skipfield
on the first iteration. This further reduces the memory use per-block of
recording down from 2 pointers in the reference implementation, to 1
size_type.
Alternatively if we go the vector-of-metadata-structs route, and don't mind doing a non-O(1) linear scan upon insert, we can linear-scan the erased-element-free-list-head metadata of each block to find blocks with erasures, subsequently eliminating additional memory use for recording blocks-with-erasures entirely. This approach would be benefited by splitting the vector-of-metadata-structs into a struct-of-vectors for each metadata item.
splice() changes our requirements:Splice requires that iterators to the source and destination hive's elements not be invalidated when the source hive's elements are transferred to the destination hive.
If we take a vector-of-pointers/vector-of-metadata approach, and our iterators use indexes into that vector, those indexes will be invalidated during splice, as the source vector's contents must be transferred into the destination vector. Further, the pointer-to-vector which the iterator must hold in order to transition between blocks, would also be invalidated during splice for iterators pointing to source elements - which means that swapping from vectors to deques and using pointers instead of indexes within the iterators, would not help.
The solution is unintuitive but functional: the iterator becomes much the same as the reference implementation: either 3 pointers, one to the block+metadata struct, one to the element and one to the skipfield, or 1 pointer (to the struct) and one index (into the element and skipfield blocks respectively). We add a "reverse-lookup" pointer into the element block's metadata which points back at the pointer pointing to it in the vector (we could have a pointer to the vector block + an index, but this consumes more memory so we'll just say a pointer to the vector position for the remainder of this text). When the iterator needs to transition blocks it follows the pointer out to the vector and increments or decrements as necessary. When splice() is run it alters the reverse-lookup pointers in each of the source's blocks such that they point to the correct pointers in the destination's vector. If the vector has to expand either during splice to accomodate the source blocks, the reverse-lookup pointers will need to be updated for all blocks.
Neither move nor swap are required to update these pointers, since those operations will simply swap the members of the vector including the pointer to the dynamically-allocated internal array, and neither the block metadata nor the iterators contain pointers to the vector itself. As such we no longer need to dynamically-allocate the vector-of-pointers in the hive and can just have it as a member.
The solution does not entirely rule out Approach B (vector of metadata structs) in the above sections, but simply means that the reverse-lookup pointer must be stored with the element block, while other metadata may be stored either with the element block, or in the vector, or in separate vectors (ie. in a struct-of-arrays style), as desired or is determined to perform well.
Also: this solution allows us to fully erase entries from the vector and relocate subsequent entries, since we're no longer relying on indexes within the iterators themselves to keep track of the block pointer location in the vector. An implementation can choose whether or not they want to consolidate the vector after a block erasure, and might want to have a maximum threshold of the number of erased entries in the vector before doing so (or possibly the number of Consecutive erased entries). This prevents the number of operations per ++/-- iterator operation from becoming too high in terms of skipping erased entries and causing latency. But more importantly, it keeps ++/-- iterator operation at O(1) amortized (and removes any performance problems relating to poor branch-prediction-recovery as described earlier).
The vector erase operation (erase_if if we're following a threshold approach and consolidating multiple erased entries at the same time) would process block metadata and adjust the reverse-lookup pointers for each block to the new values. Likewise when insertion triggers an expansion of the vector, the reverse-lookup's get updated (if a deque is used instead of a vector, the latter is unnecessary as no reallocation takes place upon insert).
Lastly, we need a way for the iterator to figure out if it's at the
beginning or end of the vector-of-pointers respectively. While we could store a
pointer to the vector itself in the block metadata as well, this is being
wasteful memory-wise. A less wasteful solution is to have 1 pointers at the beginning and end
of the vector-of-pointers which have special values ie. two pointers per hive instead of one
pointer per-block. The special value (since nullptr'ing the element block pointer is already
taken) can be the address of the pointer location itself, since this is a
unique address. If we take the alternative approach described in the summary of using the capacity metadata to indicate erased blocks instead of the pointer, we can instead use nullptr for the front and back pointers.
Now we lack a group_number metadata entry but we also lack a way to obtain the group number from the vector-of-pointers, since neither the block metadata nor the iterator currently store a pointer to the vector (and the iterator can't, since the pointer might get invalidated and the iterator can't get automatically updated by the container).
Luckily however, we don't need to know the group number for these operations to
work; we only need to know if one group is later in the sequence than the
other, and since we're storing a reverse-lookup pointer to the pointer in the
vector-of-pointers, when comparing to see if it1 < it2 we only
need to check whether it1->block_metadata->reverse-lookup <
it2->block_metadata->reverse-lookup.
If we use a deque-of-pointers-to-blocks instead of a vector we can't do the above, as the pointers are not guaranteed to point to locations within the same block. So for a deque we need have to store pointers to the deque in each block in order to get block numbers, which as mentioned is wasteful. We could however remove the back and front pointers in the deque-of-pointers at that point, as the iterator could use the pointer to the vector to find the front and back of the deque, instead.
That's all. This is probably not the only approach possible when not using the reference implementation, but it certainly will work.