The purpose of a container in the standard library cannot be to provide the optimal solution for all scenarios. Inevitably in fields such as high-performance trading or gaming, the optimal solution within critical loops will be a custom-made one that fits that scenario perfectly. However, outside of the most critical of hot paths, there is a wide range of application for more generalized solutions.
Hive is a formalisation, extension and optimization of what is typically known as a 'bucket array' container in game programming circles; similar structures exist in various incarnations across the high-performance computing, high performance trading, 3D simulation, physics simulation, robotics, server/client application and particle simulation fields (see: https://groups.google.com/a/isocpp.org/forum/#!topic/sg14/1iWHyVnsLBQ).
The concept of a bucket array is: you have multiple memory blocks of elements, and a boolean token for each element which denotes whether or not that element is 'active' or 'erased', commonly known as a skipfield. If it is 'erased', it is skipped over during iteration. When all elements in a block are erased, the block is removed, so that iteration does not lose performance by having to skip empty blocks. If an insertion occurs when all the blocks are full, a new memory block is allocated.
The advantages of this structure are as follows: because a skipfield is used, no reallocation of elements is necessary upon erasure. Because the structure uses multiple memory blocks, insertions to a full container also do not trigger reallocations. This means that element memory locations stay stable and iterators stay valid regardless of erasure/insertion. This is highly desirable, for example, in game programming because there are usually multiple elements in different containers which need to reference each other during gameplay and elements are being inserted or erased in real time.
Problematic aspects of a typical bucket array are that they tend to have a fixed memory block size, do not re-use memory locations from erased elements, and utilize a boolean skipfield. The fixed block size (as opposed to block sizes with a growth factor) and lack of erased-element re-use leads to far more allocations/deallocations than is necessary. Given that allocation is a costly operation in most operating systems, this becomes important in performance-critical environments. The boolean skipfield makes iteration time complexity undefined, as there is no way of knowing ahead of time how many erased elements occur between any two non-erased elements. This can create variable latency during iteration. It also requires branching code, which may cause issues on processors with deep pipelines and poor branch-prediction failure performance.
A hive uses a non-boolean method for skipping erased elements, which allows for O(1) amortized iteration time complexity and more-predictable iteration performance than a bucket array. It also utilizes a growth factor for memory blocks and reuses erased element locations upon insertion, which leads to fewer allocations/reallocations. Because it reuses erased element memory space, the exact location of insertion is undefined, unless no erasures have occurred or an equal number of erasures and insertions have occurred (in which case the insertion location is the back of the container). The container is therefore considered unordered but sortable. Lastly, because there is no way of predicting in advance where erasures ('skips') may occur during iteration, an O(1) time complexity [ ] operator is not necessarily possible (depending on implementation) and therefore, the container is bidirectional but not random-access.
There are two patterns for accessing stored elements in a hive: the first is to iterate over the container and process each element (or skip some elements using the advance/prev/next/iterator ++/-- functions). The second is to store the iterator returned by the insert() function (or a pointer derived from the iterator) in some other structure and access the inserted element in that way. To better understand how insertion and erasure work in a hive, see the following images.
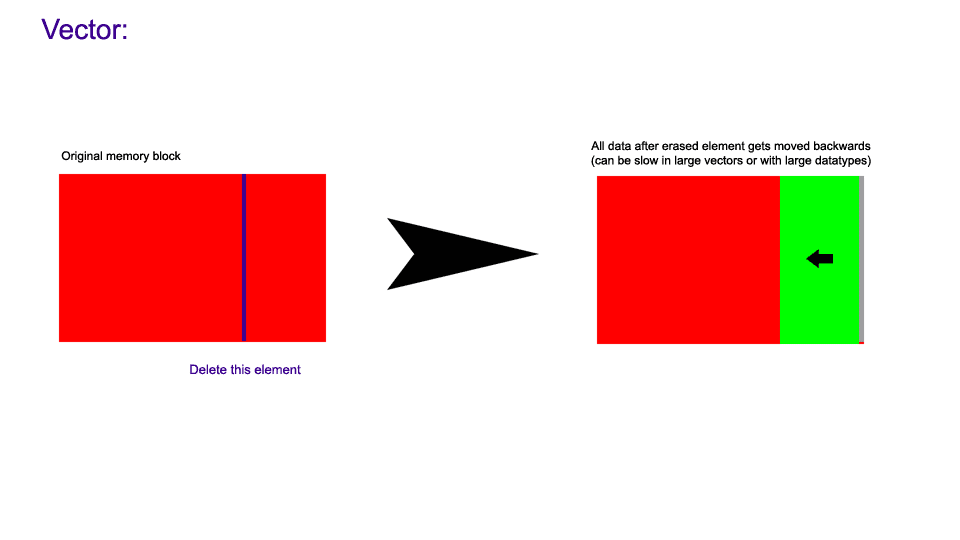
The following images demonstrate how insertion works in a hive compared to a vector when size == capacity (note: images use old name for this proposal, colony. it is the same container).

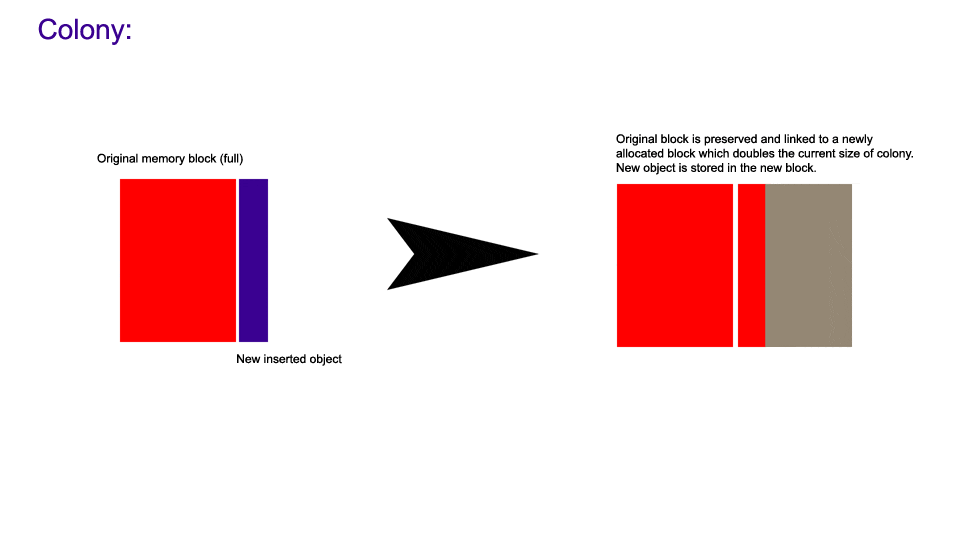
The following images demonstrate how non-back erasure works in a hive compared to a vector.
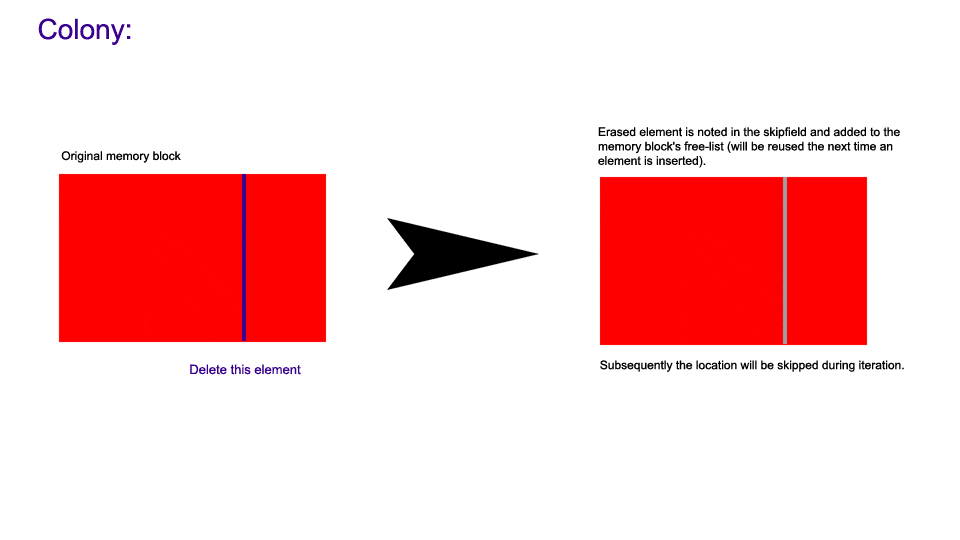
Note: Throughout this document I will use the term 'link' to denote any form of referencing between elements whether it be via ids/iterators/pointers/indexes/references/etc.
There are situations where data is heavily interlinked, iterated over frequently, and changing often. An example is the typical video game engine. Most games will have a central generic 'entity' or 'actor' class, regardless of their overall schema (an entity class does not imply an ECS). Entity/actor objects tend to be 'has a'-style objects rather than 'is a'-style objects, which link to, rather than contain, shared resources like sprites, sounds and so on. Those shared resources are usually located in separate containers/arrays so that they can re-used by multiple entities. Entities are in turn referenced by other structures within a game engine, such as quadtrees/octrees, level structures, and so on.
Entities may be erased at any time (for example, a wall gets destroyed and no longer is required to be processed by the game's engine, so is erased) and new entities inserted (for example, a new enemy is spawned). While this is all happening the links between entities, resources and superstructures such as levels and quadtrees, must stay valid in order for the game to run. The order of the entities and resources themselves within the containers is, in the context of a game, typically unimportant, so an unordered container is okay.
Unfortunately the container with the best iteration performance in the standard library, vector[1], loses pointer validity to elements within it upon insertion, and pointer/index validity upon erasure. This tends to lead to sophisticated and often restrictive workarounds when developers attempt to utilize vector or similar containers under the above circumstances.
std::list and the like are not suitable due to their poor locality, which leads to poor cache performance during iteration. This is however an ideal situation for a container such as hive, which has a high degree of locality. Even though that locality can be punctuated by gaps from erased elements, it still works out better in terms of iteration performance[1] than every existing standard library container other than deque/vector, regardless of the ratio of erased to non-erased elements.
Some more specific requirements for containers in the context of game development are listed in the appendix.
As another example, particle simulation (weather, physics etcetera) often involves large clusters of particles which interact with external objects and each other. The particles each have individual properties (spin, momentum, direction etc) and are being created and destroyed continuously. Therefore the order of the particles is unimportant, what is important is the speed of erasure and insertion. No current standard library container has both strong insertion and non-back erasure speed, so again this is a good match for hive.
Reports from other fields suggest that, because most developers aren't aware of containers such as this, they often end up using solutions which are sub-par for iterative performance such as std::map and std::list in order to preserve pointer validity, when most of their processing work is actually iteration-based. So, introducing this container would both create a convenient solution to these situations, as well as increasing awareness of better-performing approaches in general. It will also ease communication across fields, as opposed to the current scenario where each field uses a similar container but each has a different name for it.
This is purely a library addition, requiring no changes to the language.
The three core aspects of a hive from an abstract perspective are:
Each memory block houses multiple elements. The metadata about each block may or may not be allocated with the blocks themselves (could be contained in a separate structure). This metadata should include at a minimum, the number of non-erased elements within each block and the block's capacity - which allows the container to know when the block is empty and needs to be removed from the iterative chain, and also allows iterators to judge when the end of one block has been reached. A non-boolean method of skipping over erased elements during iteration while maintaining O(1) amortized iteration time complexity is required (amortized due to block traversal, which would typically require a few more operations). Finally, a mechanism for keeping track of elements which have been erased must be present, so that those memory locations can be reused upon subsequent element insertions.
The following aspects of a hive must be implementation-defined in order to allow for variance and possible performance improvement, and to conform with possible changes to C++ in the future:
However the implementation of these is significantly constrained by the requirements of the container (lack of reallocation, stable pointers to non-erased elements regardless of erasures/insertions).
In terms of the original reference implementation (current reference implementation here) the specific structure and mechanisms have changed many times over the course of development, however the interface to the container and its time complexity guarantees have remained largely unchanged (with the exception of the time complexity for updating skipfield nodes - which has not impacted significantly on performance). So it is reasonably likely that regardless of specific implementation, it will be possible to maintain this general specification without obviating future improvements in implementation, so long as time complexity guarantees for the above list are implementation-defined.
Below I explain the reference implementation's approach in terms of the three core aspects described above, along with descriptions of some alternatives implementation approaches.
In the reference implementation this is essentially a doubly-linked list of 'group' structs containing (a) a dynamically-allocated element memory block, (b) memory block metadata and (c) a dynamically-allocated skipfield. The memory blocks and skipfields have a growth factor of 2 from one group to the next. The metadata includes information necessary for an iterator to iterate over hive elements, such as the last insertion point within the memory block, and other information useful to specific functions, such as the total number of non-erased elements in the node. This approach keeps the operation of freeing empty memory blocks from the hive container at O(1) time complexity. Further information is available here.
Using a vector of group structs with dynamically-allocated element memory blocks, using the swap-and-pop idiom where groups need to be erased from the iterative sequence, would not work. To explain, when a group becomes empty of elements, it must be removed from the sequence of groups, because otherwise you end up with highly-variable latency during iteration due to the need to skip over an unknown number of empty groups when traversing from one non-empty group to the next. Simply erasing the group will not suffice, as this would create a variable amount of latency during erasure when the group becomes empty, based on the number of groups after that group which would need to be reallocated backward in the vector. But even if one swapped the to-be-erased group with the back group, and then pop'd the to-be-erased group off the back, this would not solve the problem, as iterators require a stable pointer to the group they are traversing in order to traverse to the next group in the sequence. If an iterator pointed to an element in the back group, and the back group was swapped with the to-be-erased group, this would invalidate the iterator.
A vector of pointers to group structs is more-possible. Erasing groups would still have highly-variable latency due to reallocation, however the cost of reallocating pointers may be negligible depending on architecture. While the number of pointers can be expected to be low in most cases due to the growth factor in memory blocks, if the user has defined their own memory block capacity limits the number of pointers could be large, and this has to be taken into consideration. In this case using a pop-and-swap idiom is still not possible, because while it would not necessarily invalidate the internal references of an iterator pointing to an element within the back group, the sequence of blocks would be changed and therefore the iterator would be moved backwards in the iterative sequence.
A vector of memory blocks, as opposed to a vector of pointers to memory blocks or a vector of group structs with dynamically-allocated memory blocks, would also not work, both due to the above points and because as it would (a) disallow a growth factor in the memory blocks and (b) invalidate pointers to elements in subsequent blocks when a memory block became empty of elements and was therefore removed from the vector. In short, negating hive's beneficial aspects.
The reference implementation currently uses a skipfield pattern called the Low complexity jump-counting pattern. This effectively encodes the length of runs of consecutive erased elements, into a skipfield, which allows for O(1) time complexity during iteration. Since there is no branching involved in iterating over the skipfield aside from end-of-block checks, it can be less problematic computationally than a boolean skipfield (which has to branch for every skipfield read) in terms of CPUs which don't handle branching or branch-prediction failure efficiently (eg. Core2). It also does not have the variable latency associated with a boolean skipfield.
The pattern stores and modifies the run-lengths during insertion and erasure with O(1) time complexity. It has a lot of similarities to the High complexity jump-counting pattern, which was a pattern previously used by the reference implementation. Using the High complexity jump-counting pattern is an alternative, though the skipfield update time complexity guarantees for that pattern are effectively undefined, or between O(1) and O(skipfield length) for each insertion/erasure. In practice those updates result in one memcpy operation which resolves to a single block-copy operation, but it is still a little slower than the Low complexity jump-counting pattern. The method you use to skip erased elements will typically also have an effect on the type of memory-reuse mechanism you can utilize.
A pure boolean skipfield is not usable because it makes iteration time complexity undefined - it could for example result in thousands of branching statements + skipfield reads for a single ++ operation in the case of many consecutive erased elements. In the high-performance fields for which this container was initially designed, this brings with it unacceptable latency. However another strategy using a combination of a jump-counting and boolean skipfield, which saves memory at the expense of computational efficiency, is possible as follows:
This approach has the advantage of still performing O(1) iterations from one non-erased element to the next, unlike a pure boolean skipfield approach, but compared to a pure jump-counting approach introduces 3 additional costs per iteration via (1) a branch operation when checking the bitfield, (2) an additional read (of the erased element's memory space) and (3) a bitmasking operation + bitshift to read the bit. But it does reduce the memory overhead of the skipfield to 1 bit per-element, which reduces the cache load. An implementation and benchmarking would be required in order to establish how this approach compares to the current implementation's performance.
Another method worth mentioning is the use of a referencing array - for example, having a vector of elements, together with a vector of either indexes or pointers to those elements. When an element is erased, the vector of elements itself is not updated - no elements are reallocated. Meanwhile the referencing vector is updated and the index or pointer to the erased element is erased. When iteration occurs it iterates over the referencing vector, accessing each element in the element vector via the indexes/pointers. The disadvantages of this technique are (a) much higher memory usage, particularly for small elements and (b) highly-variable latency during erasure due to reallocation in the referencing array. Since once of the goals of hive is predictable latency, this is likely not suitable.
Packed arrays are not worth mentioning as the iteration method is considered separate from the referencing mechanism, making them unsuitable for a std:: container.
There are two valid approaches here; both involve per-memory-block free lists, utilizing the memory space of erased elements. The first approach forms a free list of all erased elements. The second forms a free list of the first element in each run of consecutive erased elements ("skipblocks", in terms of the terminology used in the jump-counting pattern papers). The second can be more efficient, but requires a doubly-linked free list rather than a singly-linked free list, at least with a jump-counting skipfield - otherwise it would become an O(N) operation to update links in the skipfield, when a skipblock expands or contracts during erasure or insertion.
The reference implementation currently uses the second approach, using three things to keep track of erased element locations:
Using indexes for next and previous links, instead of pointers, reduces the necessary bit-depth of the next and previous links, thereby reducing the necessary over-alignment of the container's element type. If a global (ie. all memory blocks) free list were used, pointers would be necessary, as hive is bidirectional and does not support the [ ] operator. This would potentially increase the necessary over-alignment of the element type to 128 bits for a doubly-linked free list. A global free list would also decrease cache locality when traversing the free list by jumping between memory blocks.
Previous versions of the reference implementation used a singly-linked free list of erased elements instead of a doubly-linked free list of skipblocks. This was possible with the High complexity jump-counting pattern, but not possible using the Low complexity jump-counting pattern as it cannot calculate a skipblock's start node location from a middle node's value like the High complexity pattern can. But using free-lists of skipblocks is a more efficient approach as it requires fewer free list nodes. In addition, re-using only the start or end nodes of a skipblock is faster because it never splits a single skipblock in two (which would require adding a new skipblock to the free list).
One cannot use a stack of pointers (or similar) to erased elements for this mechanism, as early versions of the reference implementation did, because this can create allocations during erasure, which changes the exception guarantees of erase(). One could instead scan all skipfields until an erased location was found, or simply have the first item in the list above and then scan the first available block, though both of these approaches would be slow.
In terms of the alternative boolean + jump-counting skipfield approach described in the erased-element-skip-method section above, one could store both the jump-counting data and free list data in any given erased element's memory space, provided of course that elements are aligned to be wide enough to fit both.
Any iterator implementation is going to be dependent on the erased-element-skipping mechanism used. The reference implementation's iterator stores a pointer to the current 'group' struct mentioned above, plus a pointer to the current element and a pointer to its corresponding skipfield node. An alternative approach is to store the group pointer + an index, since the index can indicate both the offset from the memory block for the element, as well as the offset from the start of the skipfield for the skipfield node. However multiple implementations and benchmarks across many processors have shown this to be worse-performing than the separate pointer-based approach, despite the increased memory cost for the iterator class itself.
++ operation is as follows, utilising the reference implementation's Low-complexity jump-counting pattern:
-- operation is the same except both step 1 and 2 involve subtraction rather than adding, and step 3 checks to see if the element pointer is now before the beginning of the memory block. If so it traverses to the back of the previous group, and subtracts the value of the back skipfield node from the element pointer and skipfield pointer.
Iterators are bidirectional but also provide constant time
complexity >, <, >=, <= and <=> operators for convenience
(eg. in for loops when skipping over multiple elements per loop
and there is a possibility of going past a pre-determined end element). This is
achieved by keeping a record of the order of memory blocks. In the reference
implementation this is done by assigning a number to each memory block in its
metadata. In an implementation using a vector of pointers to memory blocks
instead of a linked list, one could use the position of the pointers within the
vector to determine this. Comparing relative order of the two iterators' memory
blocks via this number, then comparing the memory locations of the elements
themselves, if they happen to be in the same memory block, is enough to
implement all greater/lesser comparisons.
iterator insert (all variants)Insertion re-uses previously-erased element memory locations when available, so position of insertion is effectively random unless no previous erasures have occurred, in which case all elements will be inserted linearly to the back of the container, at least in the current implementation. These details have been removed from the standard in order to allow leeway for potentially-better implementations in future - though it is expected that a hive will always reuse erased memory locations, it is impossible to predict optimal strategies for unknown future hardware.
void insert (all variants)For range, fill and initializer_list insertion, it is not possible to guarantee that all the elements inserted will be sequential in the hive's iterative sequence, and therefore it is not considered useful to return an iterator to the first inserted element. There is a precedent for this in the various std:: map containers. Therefore these functions return void presently.
For range insert and range constructors, thhe syntax has been modified compared to other containers in order to take two potentially-different iterator types in order to support sentinels and the like.
iterator erase (all variants)Firstly it should be noted that erase may retain memory blocks which become completely empty of elements due to erasures, adding them to the set of unused memory blocks which are normally created by reserve(). Under what circumstances these memory blocks are retained rather than deallocated is implementation-defined - however given that small memory blocks have low cache locality compared to larger ones, from a performance perspective it is best to only retain the larger of the blocks currently allocated in the hive. In most cases this would mean the back block would almost always be retained. There is a lot of nuance to this, and it's also a matter of trading off complexity of implementation vs actual benchmarked speed vs latency. In my tests retaining both back blocks and 2nd-to-back blocks while ignoring actual capacity of blocks seems to have the best overall performance characteristics.
There are three major performance advantages to retaining back blocks as opposed to any block - the first is that these will be, under most circumstances, the largest blocks in the hive (given the built-in growth factor) - the only exception to this is when splice is used, which may result in a smaller block following a larger block (implementation-dependent). Larger blocks == more cache locality during iteration, large numbers of erased elements notwithstanding. The second advantage is that in situations where elements are being inserted to and erased from the back of the hive (this assumes no erased element locations in other memory blocks, which would otherwise be used for insertions) continuously and in quick succession, retaining the back block avoids large numbers of deallocations/reallocations. The third advantage is that deallocations of larger blocks can, in part, be moved to non-critical code regions via trim(). Though ultimately if the user wants total control of when allocations and deallocations occur they would want to use a custom allocator.
Lastly, specifying a return iterator for range-erase may seem pointless, as no reallocation of elements occurs in erase so the return iterator will almost always be the last iterator of the const_iterator first, const_iterator last pair. However if last was end(), the new value of end() (if it has changed due to empty block removal) will be returned. In this case either the user submitted end() as last, or they incremented an iterator pointing to the final element in the hive and submitted that as last. The latter is the only valid reason to return an iterator from the function, as it may occur as part of a loop which is erasing elements and ends when end() is reached. If end() is changed by the erasure of an entire memory block, but the iterator being used in the loop does not accurately reflect end()'s new value, that iterator could iterate past end() and the loop would never finish.
void reshape(std::hive_limits block_capacity_limits);This function updates the block capacity limits in the hive and, if necessary, changes any blocks which fall outside of those limits to be within the limits. For this reason it may trigger an exception with non-copyable/movable types, and also invalidate pointers/iterators/etc to elements.
The order of elements post-reshape is not guaranteed to be stable in order to allow for optimizations. Specifically in the instance where a given element memory block no longer fits within the limits supplied by the user, depending on the state of the hive as a whole, the elements within that memory block could be reallocated to previously-erased element locations in other memory blocks which do fit within the supplied limits. Or they could be reallocated to the back of the final memory block.
Additionally if there is empty capacity at the back of the last block in the container, at least some of the elements could be moved to that position rather than being reallocated to a new memory block. Both of these techniques increase cache locality by removing skipped memory spaces within existing memory blocks. However whether they are used is implementation-dependent.
void clear();User expectation was that clear() would erase all elements but not deallocate memory blocks. If deallocation of memory blocks was desired, a clear() call can be followed by a trim() call.
iterator get_iterator(pointer p) noexcept;
const_iterator get_iterator(const_pointer p) const noexcept;Because hive iterators are likely to be large, storing three
pieces of data - current memory block, current element within memory
block and potentially, current skipfield node - a program storing many
links to elements within a hive may opt to dereference iterators to
get pointers and store those instead of iterators, to save memory. This
function reverses the process, giving an iterator which can then be
used for operations such as erase. get_const_iterator was fielded as a workaround for the possibility of someone wanting to supply a non-const pointer
and get a const_iterator back, however as_const fulfills this same role when supplied to get_iterator and doesn't require expanding the interface of hive.
void shrink_to_fit();
A decision had to be made as to whether this function should, in the context of hive, be allowed to reallocate elements (as std::vector does) or simply trim off unused memory blocks (as std::deque does). Due to the fact that a large hive memory block could have as few as one remaining element after a series of erasures, it makes little sense to only trim unused blocks, and instead a shrink_to_fit is expected to reallocate all non-erased elements to as few memory blocks as possible in order to increase cache locality during iteration and reduce memory use. As with reshape(), the order of elements post-reshape is not guaranteed to be stable, to allow for potential optimizations. The trim() command is also introduced as a way to free unused memory blocks which have been previously reserved, without reallocating elements and invalidating iterators.
void sort();
It is forseen that although the container has unordered insertion, there may be circumstances where sorting is desired. Because hive uses bidirectional iterators, using std::sort or similar is not possible. Therefore an internal sort routine is warranted, as it is with std::list. An implementation of the sort routine used in the reference implementation of hive can be found in a non-container-specific form at plflib.org/indiesort.htm - see that page for the technique's advantages over the usual sort algorithms for non-random-access containers. Unfortunately to date there has been no interest in including this algorithm in the standard library. An allowance is made for sort to allocate memory if necessary, so that algorithms such as indiesort can be used internally.
void splice(hive &x);
Whether x's blocks are transferred to the beginning or
end of *this's iterative sequence, or interlaced in some way (for example, to preserve relative capacity growth-factor ordering of subsequent blocks) is implementation-defined. Better
performance may be gained in some cases by allowing the source blocks
to go to the front rather than the back, depending on how full the
final block in x's iterative sequence is. This is because
unused elements that are not at the back of hive's iterative sequence
will need to be marked as skipped, and skipping over large numbers of
elements will incur a small performance disadvantage during iteration
compared to skipping over a small number of elements, due to memory
locality.
This function is not noexcept for three reasons - the first is that a length_error exception may be thrown if any of the capacities of the source x's blocks are outside of the range defined by the destination's (*this) minimum and maximum block capacity limits. Second is that an exception may be thrown if the allocators of the two hives are different. Third is that in the case of an implementation using a linked list of group structs (ala the reference implementation) transferring blocks involves no allocation, however in the case of an implementation using a vector of pointers to blocks, an additional allocation may have to be made if the group pointer vector isn't of sufficient capacity to accomodate pointers to the spliced blocks from the source.
size_type memory() const noexcept;
A hive uses memory block metadata and may use a skipfield, both which are implementation-defined, so it is not possible for a user to estimate internal memory usage from size(), sizeof() or capacity(). This function fulfills that role. Because some types of elements may allocate their own memory dynamically (eg. std::hive<std::vector>) only the static allocation of each element is included in this functions byte count.
This function can be made constant time by adding a counter to the hive that keeps track of the number of reserved memory blocks available, or by having a vector of pointers to memory blocks instead an intrusive linked list of memory blocks. However in the case of the reference implementation which uses linked lists, the counter metadata would only be used by this function and since this function is not expected to be in heavy use, the time complexity of this function is left as implementation-defined to allow flexibility.
advance, prev and next (all variants)For these functions, complexity is dependent on state of hive, position of iterator and amount of distance, but in many cases will be less than linear, and may be constant. To explain: it is necessary in a hive to store metadata both about the capacity of each block (for the purpose of iteration) and how many non-erased elements are present within the block (for the purpose of removing blocks from the iterative chain once they become empty). For this reason, intermediary blocks between the iterator's initial block and its final destination block (if these are not the same block, and if the initial block and final block are not immediately adjacent) can be skipped rather than iterated linearly across, by using the "number of non-erased elements" metadata.
This means that the only linear time operations are any iterations within the initial block and the final block. However if either the initial or final block have no erased elements (as determined by comparing whether the block's capacity metadata and the block's "number of non-erased elements" metadata are equal), linear iteration can be skipped for that block and pointer/index math used instead to determine distances, reducing complexity to constant time. Hence the best case for this operation is constant time, the worst is linear to the distance.
distance (all variants)The same considerations which apply to advance, prev and next also apply to distance - intermediary blocks between first and last's blocks can be skipped in constant time and their "number of non-erased elements" metadata added to the cumulative distance count, while first's block and last's block (if they are not the same block) must be linearly iterated across unless either block has no erased elements, in which case the operation becomes pointer/index math and is reduced to constant time for that block. In addition, if first's block is not the same as last's block, and last is equal to end() or --end(), or is the last element in that block, last's block's elements can also counted from the "number of non-erased elements" metadata rather than via iteration.
This forms a non-binding request for the container to prioritize either performance or memory use, supplied in the form of a scoped enum. The reference implementation uses a regular un-scoped enum, as it must also work under C++03. In terms of the reference implementation the priority parameter changes the skipfield type from unsigned short (performance) to unsigned char (memory use) - which in turn changes the maximum block limits, because in the reference implementation the block capacities are limited to numeric_limits<skipfield_type>::max. The maximum block capacity limit affects iteration performance, due to a greater or lesser number of elements being able to be sequential in memory, and the subsequent effects on cache. For small numbers of elements ie. under 1000, unsigned char also will be faster in addition to needing less memory, due to the lowered cache usage and the fact that the maximum block capacity limit is not significantly limiting cache locality at this point. Hence, prioritizing for performance may not necessarily be faster in all circumstances, but should be faster in most - if in fact the request is actioned upon, and it is not guaranteed to be actioned upon in all implementations.
There is a point of diminishing returns in terms of how many elements can be stored sequentially in memory and how that impacts performance, due to the limits of cache size - hence it was found that increasing the skipfield type to unsigned int and thence increasing the block capacity limit, did not have a performance advantage on any number of elements.
In practical application the reference implementation is generally faster for insertion and (non-back) erasure than current standard library containers, and generally faster for iteration than any container except vector and deque. For full details, see benchmarks.
Suggested location of hive in the standard is 22.3, Sequence Containers.
<hive> synopsis [hive.syn]
#include <initializer_list> // see 17.10.2
#include <compare> // see 17.11.1
#include <concepts> // see 18.3
#include <stdexcept> // see 19.2
#include <utility> // see 20.2.1
#include <memory> // see 20.10
namespace std {
// 22.3.14, class template hive
struct hive_limits;
enum class hive_priority;
template <class T, class Allocator = allocator<T>, hive_priority priority = hive_priority::performance> class hive;
namespace pmr {
template <class T>
using hive = std::hive<T, polymorphic_allocator<T>>;
}
}
| All read-only operations, swap, std::swap, splice, operator= && (source), reserve, trim | Never. |
| clear, reset, operator= & (destination), operator= && (destination) | Always. |
| reshape | Only if memory blocks exist whose capacities do not fit within the supplied limits. |
| shrink_to_fit | Only if capacity() != size(). |
| erase | Only for the erased element. If an iterator is == end() it may be invalidated if the back element of the hive is erased (similar to deque (22.3.9)). Likewise if a reverse_iterator is == rend() it may be invalidated if the front element of the hive is erased. The same applies with cend() and crend() for const_iterator and const_reverse_iterator respectively. |
| insert, emplace | If an iterator is == end() or == begin() it may be invalidated by a subsequent insert/emplace. Likewise if a reverse_iterator is == rend() or == rbegin() it may be invalidated by a subsequent insert/emplace. The same rules apply with cend(), cbegin() and crend(), crbegin() for const_iterator and const_reverse_iterator respectively. |
hive [hive]hive overview [hive.overview]std::hive_limits struct with its min and
max members set to the minimum and maximum element capacity
limits respectively. The current limits in a hive instance can be
obtained from block_capacity_limits().operator[] and at member functions, which
are not provided.template <class T, class Allocator = std::allocator<T>, priority Priority = priority::performance> class hive
T - the element type. In general T shall meet the
requirements of Erasable, CopyAssignable
and CopyConstructible.
However, if emplace is utilized to insert elements into the hive, and no
functions which involve copying or moving are utilized, T is only required to
meet the requirements of Erasable.
If move-insert is utilized instead of emplace, T shall also meet the
requirements of MoveConstructible.
Allocator - an allocator that is used to acquire memory to
store the elements. The type shall meet the requirements of Allocator. The
behavior is undefined if Allocator::value_type is not the same as
T.
Priority - if set to priority::memory_use this is a non-binding request to prioritize lowered memory usage over container performance. [ Note: The request is non-binding to allow latitude for implementation-specific optimizations. If this feature is implemented, it is not specified that the container shall have better performance when using priority::performance instead of priority::memory_usage in all scenarios, but that it shall have better performance in most scenarios. - end note ]
namespace std {
struct hive_limits
{
size_t min, max;
hive_limits(size_t minimum, size_t maximum) noexcept : min(minimum), max(maximum) {}
};
enum struct hive_priority { performance, memory_use };
template <class T, class Allocator = allocator<T>, hive_priority Priority = hive_priority::performance>
class hive {
public:
// types
using value_type = T;
using allocator_type = Allocator;
using pointer = typename allocator_traits<Allocator>::pointer;
using const_pointer = typename allocator_traits<Allocator>::const_pointer;
using reference = value_type&;
using const_reference = const value_type&;
using size_type = implementation-defined; // see 22.2
using difference_type = implementation-defined; // see 22.2
using iterator = implementation-defined; // see 22.2
using const_iterator = implementation-defined; // see 22.2
using reverse_iterator = implementation-defined; // see 22.2
using const_reverse_iterator = implementation-defined; // see 22.2
hive() noexcept(noexcept(Allocator())) : hive(Allocator()) { }
explicit hive(std::hive_limits block_capacity_limits) noexcept(noexcept(Allocator())) : hive(Allocator()) { }
explicit hive(const Allocator&) noexcept;
explicit hive(std::hive_limits block_capacity_limits, const Allocator&) noexcept;
explicit hive(size_type n, std::hive_limits block_capacity_limits = implementation-defined, const Allocator& = Allocator());
hive(size_type n, const T& value, std::hive_limits block_capacity_limits = implementation-defined, const Allocator& = Allocator());
template<class InputIterator1, class InputIterator2>
hive(InputIterator1 first, InputIterator2 last, std::hive_limits block_capacity_limits = implementation-defined, const Allocator& = Allocator());
hive(const hive& x);
hive(hive&&) noexcept;
hive(const hive&, const Allocator&);
hive(hive&&, const Allocator&);
hive(initializer_list<T>, std::hive_limits block_capacity_limits = implementation-defined, const Allocator& = Allocator());
~hive() noexcept;
hive& operator= (const hive& x);
hive& operator= (hive&& x) noexcept(allocator_traits<Allocator>::propagate_on_container_move_assignment::value || allocator_traits<Allocator>::is_always_equal::value);
hive& operator= (initializer_list<T>);
template<class InputIterator1, class InputIterator2> void assign(InputIterator1 first, InputIterator2 last);
void assign(size_type n, const T& t);
void assign(initializer_list<T>);
allocator_type get_allocator() const noexcept;
// iterators
iterator begin() noexcept;
const_iterator begin() const noexcept;
iterator end() noexcept;
const_iterator end() const noexcept;
reverse_iterator rbegin() noexcept;
const_reverse_iterator rbegin() const noexcept;
reverse_iterator rend() noexcept;
const_reverse_iterator rend() const noexcept;
const_iterator cbegin() const noexcept;
const_iterator cend() const noexcept;
const_reverse_iterator crbegin() const noexcept;
const_reverse_iterator crend() const noexcept;
// capacity
[[nodiscard]] bool empty() const noexcept;
size_type size() const noexcept;
size_type max_size() const noexcept;
size_type capacity() const noexcept;
size_type memory() const noexcept;
void reserve(size_type n);
void shrink_to_fit();
void trim() noexcept;
// modifiers
template <class... Args> iterator emplace(Args&&... args);
iterator insert(const T& x);
iterator insert(T&& x);
void insert(size_type n, const T& x);
template <class InputIterator1, class InputIterator2> void insert(InputIterator1 first, InputIterator2 last);
void insert(initializer_list<T> il);
iterator erase(const_iterator position);
iterator erase(const_iterator first, const_iterator last);
void swap(hive&) noexcept(allocator_traits<Allocator>::propagate_on_container_swap::value || allocator_traits<Allocator>::is_always_equal::value);
void clear() noexcept;
// hive operations
void splice(hive &x);
std::hive_limits block_capacity_limits() const noexcept;
void reshape(std::hive_limits block_capacity_limits);
iterator get_iterator(pointer p) noexcept;
const_iterator get_iterator(const_pointer p) const noexcept;
void sort();
template <class Compare> void sort(Compare comp);
friend bool operator== (const hive &x, const hive &y);
friend bool operator!= (const hive &x, const hive &y);
class iterator
{
friend void advance(iterator &it, Distance n);
friend iterator next(iterator it, difference_type distance = 1);
friend iterator prev(iterator it, difference_type distance = 1);
friend difference_type distance(iterator first, iterator last);
}
class const_iterator
{
friend void advance(const_iterator &it, Distance n);
friend const_iterator next(const_iterator it, difference_type distance = 1);
friend const_iterator prev(const_iterator it, difference_type distance = 1);
friend difference_type distance(const_iterator first, const_iterator last);
}
class reverse_iterator
{
friend void advance(reverse_iterator &it, Distance n);
friend reverse_iterator next(reverse_iterator it, difference_type distance = 1);
friend reverse_iterator prev(reverse_iterator it, difference_type distance = 1);
friend difference_type distance(reverse_iterator first, reverse_iterator last);
}
class const_reverse_iterator
{
friend void advance(const_reverse_iterator &it, Distance n);
friend const_reverse_iterator next(const_reverse_iterator it, difference_type distance = 1);
friend const_reverse_iterator prev(const_reverse_iterator it, difference_type distance = 1);
friend difference_type distance(const_reverse_iterator first, const_reverse_iterator last);
}
// swap
friend void swap(hive& x, hive& y)
noexcept(noexcept(x.swap(y)));
// erase
template <class Predicate>
friend size_type erase_if(hive& c, Predicate pred);
template <class U>
friend size_type erase(hive& c, const U& value);
}
template<class InputIterator, class Allocator = allocator<iter-value-type <InputIterator>>>
hive(InputIterator, InputIterator, Allocator = Allocator())
-> hive<iter-value-type <InputIterator>, Allocator>;
explicit hive(const Allocator&);
explicit hive(size_type n, const T& value, std::hive_limits block_capacities = implementation-defined, const Allocator& =Allocator());
T shall be Cpp17MoveInsertable into
*this.value, using
the specified allocator.length_error if block_capacities.min or
block_capacities.max are outside the implementation's minimum
and maximum element memory block capacity limits, or if
block_capacities.min > block_capacities.max.
n is larger than
block_capacities.min, the capacity of the first block created
will be the smaller of n or block_capacities.max.template <class InputIterator1, class InputIterator2>
hive(InputIterator1 first, InputIterator2 last, std::hive_limits block_capacities = implementation-defined, const Allocator& = Allocator());InputIterator1 shall be std::equality_comparable_with InputIterator2.length_error if block_capacities.min or
block_capacities.max are outside the implementation's minimum
and maximum element memory block capacity limits, or if
block_capacities.min > block_capacities.max. Or
n be last -
first; if n is larger than block_capacities.min,
the capacity of the first block created will be the smaller of
n or block_capacities.max.size_type capacity() const noexcept;
size_type memory() const noexcept;
void reserve(size_type n);
reserve(), capacity() is not guaranteed to be
equal to the argument of reserve(), may be greater. Does not
cause reallocation of elements.(n / block_capacity_limits().max) + 1 allocations.length_error if n > max_size()223.223) reserve() uses Allocator::allocate() which may throw an appropriate exception.
void shrink_to_fit();
T is Cpp17MoveInsertable into
*this.capacity() to be closer to size(). [ Note: The
request is non-binding to allow latitude for implementation-specific
optimizations. - end note ] It does not increase capacity(),
but may reduce capacity() by causing reallocation. It may move
elements from multiple memory blocks and consolidate them into a smaller
number of memory blocks.void trim();
reserve(), clear() or erase(). If such memory
blocks are present, capacity() will be reduced.iterator insert(const T& x);
iterator insert(T&& x);
void insert(size_type n, const T& x);
template <class InputIterator1, class InputIterator2>
void insert(InputIterator1 first, InputIterator2 last);
void insert(initializer_list<T>);
template <class... Args>
iterator emplace(Args&&... args);template <class InputIterator1, class InputIterator2> void insert(InputIterator1 first, InputIterator2 last), InputIterator1 shall be std::equality_comparable_with InputIterator2.T. Insertion of
multiple elements into a hive is linear in the number of elements
inserted, and the number of calls to the copy constructor or move
constructor of T is exactly equal to the number of elements
inserted.end(), in which case it may be
invalidated. Likewise if a reverse_iterator points to rend()
it may be invalidated. If an exception is thrown there are no effects.iterator erase(const_iterator position);
iterator erase(const_iterator first, const_iterator last);
end() and
the back element of the hive is erased, that iterator may be invalidated.
Likewise if a reverse_iterator is equal to rend() and the
front element of the hive is erased, that reverse_iterator may be
invalidated.void swap(hive& x) noexcept(allocator_traits<Allocator>::propagate_on_container_swap::value || allocator_traits<Allocator>::is_always_equal::value);
capacity() of
*this with that of x.void clear();
void splice(hive &x);
x into *this
and x becomes empty. Pointers and references to the moved
elements of x now refer to those same elements but as members
of *this. Iterators referring to the moved elements will
continue to refer to their elements, but they now behave as iterators into
*this, not into x.length_error if any of x's element memory block capacities are outside the current minimum and maximum element
memory block capacity limits of *this.223std::hive_limits block_capacity_limits() const noexcept;
min and
max members set to the current minimum and maximum element
memory block capacity limits of *this.void reshape(std::hive_limits block_capacity_limits);T shall be Cpp17MoveInsertable into
*this.length_error if block_capacities.min or
block_capacities.max are outside the implementation's minimum
and maximum element memory block capacity limits, or if
block_capacities.min > block_capacities.max.223iterator get_iterator(pointer p) noexcept;
const_iterator get_iterator(const_pointer p) const noexcept;
p does not point to an element in
*this, end() is returned.void sort();
template <class Compare>
void sort(Compare comp);T is Cpp17MoveInsertable into
*this.operator < or
a Compare function object. If an exception is thrown, the
order of the elements in *this is unspecified. Iterators and
references may be invalidated.N == size().bad_alloc if it fails to allocate any memory necessary for the sort process.friend void swap(hive &x, hive &y) noexcept(noexcept(x.swap(y)));x.swap(y).friend bool operator== (const hive &x, const hive &y);
friend bool operator!= (const hive &x, const hive &y);True if both containers have the same elements in the same iterative sequence, otherwise False.
For !=, returns True if both containers do not have the same elements in the same iterative sequence, otherwise False.
class iterator
{
friend void advance(iterator &it, Distance n);
friend iterator next(iterator it, difference_type distance = 1);
friend iterator prev(iterator it, difference_type distance = 1);
friend difference_type distance(iterator first, iterator last);
}
class const_iterator
{
friend void advance(const_iterator &it, Distance n);
friend const_iterator next(const_iterator it, difference_type distance = 1);
friend const_iterator prev(const_iterator it, difference_type distance = 1);
friend difference_type distance(const_iterator first, const_iterator last);
}
class reverse_iterator
{
friend void advance(reverse_iterator &it, Distance n);
friend reverse_iterator next(reverse_iterator it, difference_type distance = 1);
friend reverse_iterator prev(reverse_iterator it, difference_type distance = 1);
friend difference_type distance(reverse_iterator first, reverse_iterator last);
}
class const_reverse_iterator
{
friend void advance(const_reverse_iterator &it, Distance n);
friend const_reverse_iterator next(const_reverse_iterator it, difference_type distance = 1);
friend const_reverse_iterator prev(const_reverse_iterator it, difference_type distance = 1);
friend difference_type distance(const_reverse_iterator first, const_reverse_iterator last);
}
template <class U>
friend size_type erase(hive& c, const U& value);value are erased. Invalidates all references and iterators to the erased elements.template <class Predicate>
friend size_type erase_if(hive& c, Predicate pred);pred are erased. Invalidates all references and iterators to the erased elements.Matt would like to thank: Glen Fernandes and Ion Gaztanaga for restructuring
advice, Robert Ramey for documentation advice, various Boost and SG14 members for support, critiques and corrections, Baptiste Wicht for teaching me how to construct decent benchmarks, Jonathan Wakely, Sean Middleditch, Jens Maurer (very nearly a co-author at this point really),
Patrice Roy and Guy Davidson for standards-compliance advice and critiques, support, representation at meetings and bug reports, Henry Miller for getting me to clarify why the instrusive list/free list approach to memory location reuse is the most appropriate, Ville Voutilainen and Gasper Azman for help with the colony/hive rename paper, that ex-Lionhead guy for annoying me enough to force me to implement the original skipfield pattern, Jon Blow for some initial advice and Mike Acton for some influence, the community at large for giving me feedback and bug reports on the reference implementation.
Also Nico Josuttis for doing such a great job in terms of explaining the general format of the structure to the committee.
Using reference implementation.
#include <iostream>
#include <numeric>
#include "plf_hive.h"
int main(int argc, char **argv)
{
plf::hive<int> i_hive;
// Insert 100 ints:
for (int i = 0; i != 100; ++i)
{
i_hive.insert(i);
}
// Erase half of them:
for (plf::hive<int>::iterator it = i_hive.begin(); it != i_hive.end(); ++it)
{
it = i_hive.erase(it);
}
std::cout << "Total: " << std::accumulate(i_hive.begin(), i_hive.end(), 0) << std::endl;
std::cin.get();
return 0;
} #include <iostream>
#include "plf_hive.h"
int main(int argc, char **argv)
{
plf::hive<int> i_hive;
plf::hive<int>::iterator it;
plf::hive<int *> p_hive;
plf::hive<int *>::iterator p_it;
// Insert 100 ints to i_hive and pointers to those ints to p_hive:
for (int i = 0; i != 100; ++i)
{
it = i_hive.insert(i);
p_hive.insert(&(*it));
}
// Erase half of the ints:
for (it = i_hive.begin(); it != i_hive.end(); ++it)
{
it = i_hive.erase(it);
}
// Erase half of the int pointers:
for (p_it = p_hive.begin(); p_it != p_hive.end(); ++p_it)
{
p_it = p_hive.erase(p_it);
}
// Total the remaining ints via the pointer hive (pointers will still be valid even after insertions and erasures):
int total = 0;
for (p_it = p_hive.begin(); p_it != p_hive.end(); ++p_it)
{
total += *(*p_it);
}
std::cout << "Total: " << total << std::endl;
if (total == 2500)
{
std::cout << "Pointers still valid!" << std::endl;
}
std::cin.get();
return 0;
} Benchmark results for the hive reference implementation under GCC on an Intel Xeon E3-1241 (Haswell) are here.
Old benchmark results for an earlier version of hive under MSVC 2015 update 3, on an Intel Xeon E3-1241 (Haswell) are here. There is no commentary for the MSVC results.
As mentioned, it is worthwhile for performance reasons in situations where the order of container elements is not important and:
Under these circumstances a hive will generally out-perform other std:: containers. In addition, because it never invalidates pointer references to container elements (except when the element being pointed to has been previously erased) it may make many programming tasks involving inter-relating structures in an object-oriented or modular environment much faster, and could be considered in those circumstances.
Some ideal situations to use a hive: cellular/atomic simulation, persistent octtrees/quadtrees, game entities or destructible-objects in a video game, particle physics, anywhere where objects are being created and destroyed continuously. Also, anywhere where a vector of pointers to dynamically-allocated objects or a std::list would typically end up being used in order to preserve pointer stability but where order is unimportant.
A deque is reasonably dissimilar to a hive - being a double-ended queue, it requires a different internal framework. In addition, being a random-access container, having a growth factor for memory blocks in a deque is problematic (though not impossible). A deque and hive have no comparable performance characteristics except for insertion (assuming a good deque implementation). Deque erasure performance varies wildly depending on the implementation, but is generally similar to vector erasure performance. A deque invalidates pointers to subsequent container elements when erasing elements, which a hive does not, and guarantees ordered insertion.
Unlike a std::vector, a hive can be read from and inserted into at the same time (assuming different locations for read and write), however it cannot be iterated over and written to at the same time. If we look at a (non-concurrent implementation of) std::vector's thread-safe matrix to see which basic operations can occur at the same time, it reads as follows (please note push_back() is the same as insertion in this regard):
| std::vector | Insertion | Erasure | Iteration | Read |
| Insertion | No | No | No | No |
| Erasure | No | No | No | No |
| Iteration | No | No | Yes | Yes |
| Read | No | No | Yes | Yes |
In other words, multiple reads and iterations over iterators can happen simultaneously, but the potential reallocation and pointer/iterator invalidation caused by insertion/push_back and erasure means those operations cannot occur at the same time as anything else.
Hive on the other hand does not invalidate pointers/iterators to non-erased elements during insertion and erasure, resulting in the following matrix:
| hive | Insertion | Erasure | Iteration | Read |
| Insertion | No | No | No | Yes |
| Erasure | No | No | No | Mostly* |
| Iteration | No | No | Yes | Yes |
| Read | Yes | Mostly* | Yes | Yes |
* Erasures will not invalidate iterators unless the iterator points to the erased element.
In other words, reads may occur at the same time as insertions and erasures (provided that the element being erased is not the element being read), multiple reads and iterations may occur at the same time, but iterations may not occur at the same time as an erasure or insertion, as either of these may change the state of the skipfield which is being iterated over, if a skipfield is used in the implementation. Note that iterators pointing to end() may be invalidated by insertion.
So, hive could be considered more inherently thread-safe than a (non-concurrent implementation of) std::vector, but still has some areas which would require mutexes or atomics to navigate in a multithreaded environment.
Because erased-element memory locations may be reused by
insert() and emplace(), insertion position is
essentially random unless no erasures have been made, or an equal number of
erasures and insertions have been made.
One reason might be to ensure that memory blocks match a certain processor's cache or memory pathway sizes. Another reason to do this is that it is slightly slower to obtain an erased-element location from the list of groups-with-erasures (subsequently utilising that group's free list of erased locations) and to reuse that space than to insert a new element to the back of the hive (the default behavior when there are no previously-erased elements). If there are any erased elements in active memory blocks at the moment of insertion, hive will recycle those memory locations.
So if a block size is large, and many erasures occur but the block is not completely emptied, iterative performance might suffer due to large memory gaps between any two non-erased elements and subsequent drop in data locality and cache performance. In that scenario you may want to experiment with benchmarking and limiting the minimum/maximum sizes of the blocks, such that memory blocks are freed earlier and find the optimal size for the given use case.
Though I am happy to be proven wrong I suspect hives/colonies/bucket arrays are their own abstract data type. Some have suggested it's ADT is of type bag, I would somewhat dispute this as it does not have typical bag functionality such as searching based on value (you can use std::find but it's o(n)) and adding this functionality would slow down other performance characteristics. Multisets/bags are also not sortable (by means other than automatically by key value). hive does not utilize key values, is sortable, and does not provide the sort of functionality frequently associated with a bag (e.g. counting the number of times a specific value occurs).
Two reasons:
++
and -- iterator operations become undefined in terms of
time complexity, making them non-compliant with the C++ standard. At
the moment they are O(1) amortized, in the reference implementation this constitutes typically one update for both
skipfield and element pointers, but two if a skipfield jump takes the
iterator beyond the bounds of the current block and into the next
block. But if empty blocks are allowed, there could be anywhere between
1 and std::numeric_limits<size_type>::max empty
blocks between the current element and the next. Essentially you get
the same scenario as you do when iterating over a boolean skipfield. It
would be possible to move these to the back of the hive as trailing
blocks, or house them in a separate list or vector for future usage,
but this may create performance issues if any of the blocks are not at
their maximum size (see below).The default scenario, for reasons of predictability, should be to free the memory block in most cases. However for the reasons described in the design decisions section on erase(), retaining the back block at least has performance and latency benefits. Therefore retaining no memory blocks is non-optimal in cases where the user is not using a custom allocator. Meanwhile, retaining All memory blocks is bad for performance as many small memory blocks will be retained, which decreases iterative performance due to lower cache locality. However, one perspective is that if a scenario calls for retaining memory blocks instead of deallocating them, this should be left to an allocator to manage. Otherwise you get unpredictable memory behavior across implementations, and this is one of the things that SG14 members have complained about consistently with STL implementations. This is currently an open topic for discussion.
While implementations are free to chose their own limits and strategies here, in the reference implementation memory block sizes start from either the dynamically-defined default minimum size (8 elements, larger if the type stored is small) or an amount defined by the end user (with a minimum of 3 elements, as there is enough metadata per-block that less than 3 elements is generally a waste of memory unless the value_type is extremely large). Subsequent block sizes then increase the total capacity of the hive by a factor of 2 (so, 1st block 8 elements, 2nd 8 elements, 3rd 16 elements, 4th 32 elements etcetera) until the maximum block size is reached. The default maximum block size in the reference implementation is the maximum possible number that the skipfield bitdepth is capable of representing (std::numeric_limits<skipfield_type>::max()). By default the skipfield bitdepth is 16 so the maximum size of a block would be 65535 elements in that context.
The skipfield bitdepth was initially a template parameter which could be set to
any unsigned integer - unsigned char, unsigned int, Uint_64, etc. Unsigned
short (guaranteed to be at least 16 bit, equivalent to C++11's
uint_least16_t type) was found to have the best performance in real-world
testing on x86 and x86_64 platforms due to the balance between memory contiguousness, memory waste and
the number of allocations. unsigned char was found to have better performance below 1000 elements and of course lower memory use. Other platforms have not been tested. Since only two values were considered useful, they've been replaced in newer versions by a priority parameter, which specifies whether the priority of the instantiation is memory use or performance. While this is not strictly true in the sense that unsigned char will also have better performance for under 1000 elements, it is a compromise in order to have the implementation reflect a standard which may enable other implementations which do not share the same performance characteristics.
No and yes. Yes if you're careful, no if you're not.
On platforms which support scatter and gather operations via hardware (e.g.
AVX512) you can use hive with SIMD as much as you want, using gather to
load elements from disparate or sequential locations, directly into a SIMD
register, in parallel. Then use scatter to push the post-SIMD-process
values elsewhere after. On platforms which do not support this in hardware,
you would need to manually implement a scalar gather-and-scatter operation
which may be significantly slower.
In situations where gather and scatter operations are too expensive, which require elements to be contiguous in memory for SIMD processing, this is more complicated. When you have a bunch of erasures in a hive, there's no guarantee that your objects will be contiguous in memory, even though they are sequential during iteration. Some of them may also be in different memory blocks to each other. In these situations if you want to use SIMD with hive, you must do the following:
Generally if you want to use SIMD without gather/scatter, it's probably preferable to use a vector or an array.
See D2332R0.
As noted the container was originally designed for highly object-oriented situations where you have many elements in different containers linking to many other elements in other containers. This linking can be done with pointers or iterators in hive (insert returns an iterator which can be dereferenced to get a pointer, pointers can be converted into iterators with the supplied functions (for erase etc)) and because pointers/iterators stay stable regardless of insertion/erasure, this usage is unproblematic. You could say the pointer is equivalent to a key in this case (but without the overhead). That is the first access pattern, the second is straight iteration over the container, as you say. Secondly, the container does have (typically better than O(n)) advance/next/prev implementations, so multiple elements can be skipped.
While technically a non-binding request, this parameter promotes the use of the container in heavily
memory-constrained environments like embedded programming. In the context of the reference implementation this means switching the skipfield type from unsigned short to unsigned char, in other implementations it could mean something else.
See more explanation in V. Technical Specifications.
Unfortunately this parameter also means operator=, swap and some
other functions won't work between hives of the same type but with differing priorities.
I'm not really sure how to answer this, as I don't see the resemblance, unless you count maps, vectors etc as being allocators also. The only aspect of it which resembles what an allocator might do, is the memory re-use mechanism. It would be impossible for an allocator to perform a similar function while still allowing the container to iterate over the data linearly in memory, preserving locality, in the manner described in this document.
This is true for many/most AAA game companies who are on the bleeding edge, but they also do this for vector etc, so they aren't the target audience of std:: for the most part; sub-AAA game companies are more likely to use third party/pre-existing tools. As mentioned earlier, this structure (bucket-array-like) crops up in many, many fields, not just game dev. So the target audience is probably everyone other than AAA gaming, but even then, it facilitates communication across fields and companies as to this type of container, giving it a standardized name and understanding.
The only current analysis has been around the question of whether it's possible for this specification to fail to allow for a better implementation in future. This is unlikely given the container's requirements and how this impacts on implementation. Bucket arrays have been around since the 1990s, there's been no significant innovation in them until now. I've been researching/working on hive since early 2015, and while I can't say for sure that a better implementation might not be possible, I am confident that no change should be necessary to the specification to allow for future implementations, if it is done correctly.
The requirement of allowing no reallocations upon insertion or erasure, truncates possible implementation strategies significantly. Memory blocks have to be independently allocated so that they can be removed (when empty) without triggering reallocation of subsequent elements. There's limited numbers of ways to do that and keep track of the memory blocks at the same time. Erased element locations must be recorded (for future re-use by insertion) in a way that doesn't create allocations upon erasure, and there's limited numbers of ways to do this also. Multiple consecutive erased elements have to be skipped in O(1) time, and again there's limits to how many ways you can do that. That covers the three core aspects upon which this specification is based. See IV. Design Decisions for the various ways these aspects can be designed.
The time complexity of updates to whatever erased-element skipping mechanism is used should, I think, be left implementation-defined, as defining time complexity may obviate better solutions which are faster but are not necessarily O(1). These updates would likely occur during erasure, insertion, splicing and container copying.
While this would statistically ensure that smaller blocks get deallocated first due to becoming empty faster than later blocks, it introduces uncertain latency issues during insert, particularly when custom memory block sizes are used and the number of elements is large. With the current implementation there is an intrusive list of blocks with erasures, and within each block's metadata there's a free list of skipblocks. When reusing the current head of the intrusive list determines the block, and the current head of that block's free list determines the skipblock to be reused. This means that the most recently erased element will be the first to reused. This works out well for two reasons: currently-contiguous sequences of elements will tend to stay that way, helping cache coherence, and when elements are erased and inserted in sequence those erased memory locations will tend to be already in the cache when inserting. Lastly, this structure involves a minimum of branching and checks, resulting in minimal latency during insertion and erasure.
Here are some more specific requirements with regards to game engines, verified by game developers within SG14:
std::vector in its default state does not meet these requirements due to:
Game developers therefore either develop custom solutions for each scenario or implement workarounds for vector. The most common workarounds are most likely the following or derivatives:
Hive brings a more generic solution to these contexts. While some developers, particularly AAA developers, will almost always develop a custom solution for specific use-cases within their engine, I believe most sub-AAA and indie developers are more likely to rely on third party solutions. Regardless, standardising the container will allow for greater cross-discipline communication.
One of the requirements of hive is that pointers to non-erased elements stay valid regardless of insertion/erasure within the container. For this reason the container must use multiple memory blocks. If a single memory block were used, like in a std::vector, reallocation of elements would occur when the container expanded (and the elements were copied to a larger memory block). Instead, hive will insert into existing memory blocks when able, and create a new memory block when all existing memory blocks are full. This keeps insertion at O(1).
Multiple insertions may allow an implementation to reserve suitably-sized memory blocks in advance, reducing the number of allocations necessary (whereas singular insertion would generally follow the implementation's block growth pattern, possibly allocating more than necessary). However when it comes to time complexity it has no advantages over singular insertion, is linear to the number elements inserted.
Erasure is a simple matter of destructing the element in question and updating whatever data is associated with the erased-element skipping mechanism eg. the skipfield. Since we use a skipping mechanism to avoid erasures during iterator, no reallocation of subsequent elements is necessary and the process is O(1). Additionally, when using a Low-complexity jump-counting pattern the skipfield update is also always O(1).
Note: When a memory block becomes empty of non-erased elements it must be freed to the OS (or reserved for future insertions, depending on implementation) and removed from the hive's sequence of memory blocks. It it was not, we would end up with non-O(1) iteration, since there would be no way to predict how many empty memory blocks there would be between the current memory block being iterated over, and the next memory block with non-erased (active) elements in it.
In this case, where the element is non-trivially destructible, the time complexity is O(N), with infrequent deallocation necessary from the removal of an empty memory block as noted above. However where the elements are trivially-destructible, if the range spans an entire memory block at any point, that block and it's metadata can simply be removed without doing any individual writes to it's metadata or individual destruction of elements, potentially making this a O(1) operation.
In addition (when dealing with trivially-destructible types) for those memory blocks where only a portion of elements are erased by the range, if no prior erasures have occurred in that memory block you may be able to erase that range in O(1) time, as, for example, if you are using a skipfield there will be no need to check the skipfield within the range for previously erased elements. The reason you would need to check for previously erased elements within that portion's range is so you can update the metadata for that memory block to accurately reflect how many non-erased elements remain within the block. The non-erased element-count metadata is necessary because there is no other way to ascertain when a memory block is empty of non-erased elements, and hence needs to be removed from the hive's iteration sequence. The reasoning for why empty memory blocks must be removed is included in the Erase(single) section, above.
However in most cases the erase range will not perfectly match the size of all memory blocks, and with typical usage of a hive there is usually some prior erasures in most memory blocks. So, for example, when dealing with a hive of a trivially-destructible type, you might end up with a tail portion of the first memory block in the erasure range being erased in O(N) time, the second and intermediary memory block being completely erased and freed in O(1) time, and only a small front portion of the third and final memory block in the range being erased in O(N) time. Hence the time complexity for trivially-destructible elements approximates O(log n) on average, being between O(1) and O(N) depending on the start and end of the erasure range.
This relies on basic iteration so is O(N).
Hive only does full-container splicing, not partial-container splicing (use range-insert with std::make_move_iterator to achieve the latter, albiet with the loss of pointer validity to the moved range). When splicing, the memory blocks from the source hive are transferred to the destination hive without processing the individual elements. These blocks may either be placed at the front of the hive or the end, depending on how full the source back block is compared to the destination back block. If the destination back block is more full ie. there is less unused space in it, it is better to put it at the beginning of the source block - as otherwise this creates a larger gap to skip during iteration which in turn affects cache locality. If there are unused element memory spaces at the back of the destination container (ie. the final memory block is not full) and a skipfield is used, the skipfield nodes corresponding to those empty spaces must be altered to indicate that these are skipped elements.
Generally the time complexity is O(1), and if a skipfield pattern is used it must allow for O(1) skipping of multiple erased elements. However every so often iteration will involve a transistion to the next/previous memory block in the hive's sequence of blocks, depending on whether we are doing ++ or --. At this point a read of the next/previous memory block's corresponding skipfield would be necessary, in case the front/back element(s) in that memory block are erased and hence skipped. So for every block transition, 2 reads of the skipfield are necessary instead of 1. Hence the time complexity is O(1) amortized.
If skipfields are used they must be per-element-memory-block and independent of subsequent/previous memory blocks, as otherwise you end up with a vector for a skipfield, which would need a range erased every time a memory block was removed from the hive (see notes under Erase, above), and reallocation to a larger skipfield memory block when a hive expanded. Both of these procedures carry reallocation costs, meaning you could have thousands of skipfield nodes needing to be reallocated based on a single erasure (from within a memory block which only had one non-erased element left and hence would need to be removed from the hive). This is unacceptable latency for any field involving high timing sensitivity (all of SG14).
For any implementation these should generally be stored as member variables and so returning them is O(1).
The reasoning for this is similar to that of Erase(multiple), above.
Complexity is dependent on state of hive, position of iterator and length of
distance, but in many cases will be less than linear. It is
necessary in a hive to store metadata both about the capacity of each block
(for the purpose of iteration) and how many non-erased elements are present
within the block (for the purpose of removing blocks from the iterative chain
once they become empty). For this reason, intermediary blocks between the
iterator's initial block and its final destination block (if these are not the
same block, and if the initial block and final block are not immediately
adjacent) can be skipped rather than iterated linearly across, by subtracting
the "number of non-erased elements" metadata from distance for
those blocks.
This means that the only linear time operations are any iterations within the initial block and the final block. However if either the initial or final block have no erased elements (as determined by comparing whether the block's capacity metadata and the block's "number of non-erased elements" metadata are equal), linear iteration can be skipped for that block and pointer/index math used instead to determine distances, reducing complexity to constant time. Hence the best case for this operation is constant time, the worst is linear to the distance.
The same considerations which apply to advance, prev and next also apply to distance - intermediary blocks between iterator1 and iterator2's blocks can be skipped in constant time, if they exist. iterator1's block and iterator2's block (if these are not the same block) must be linearly iterated across using ++ unless either block has no erased elements, in which case the operation becomes pointer/index math and is reduced to constant time for that block. In addition, if iterator1's block is not the same as iterator2's block, and iterator2 is equal to end() or (end() - 1), or is the last element in that block, iterator2's block's elements can also counted from the metadata rather than iteration.
I am somewhat awkwardly forced into a position where I have to question and push back slightly against the current enthusiasm around constexpr containers. At the time of writing there are no compilers which both support constexpr non-trivial destructors and also have a working implementation of a constexpr container. Until that is remedied, we won't really know what we're dealing with. My own testing in terms of making hive functions constexpr has not been encouraging. 2% performance decrease in un-altered benchmark code was common, and I suspect the common cause of this was the caching of return values from functions called at compile-time when it was cheaper to calculate them on-the-fly than to return them from main memory. This suspicion was based on the substantial increases in executable size in the constexpr versions. It is also a well-known situation in modern game development.
For an example of the latter, think about size() in std::vector. This can be calculated in most implementations by (vector.end_iterator.pointer - vector.memory_block), both of which will most likely be in cache at the time of calling size(). That's if size isn't a member variable or something. Calculating a minus operation on stuff that's already in cache is about 100x faster than making a call out to main memory for a compile-time-stored value of this function, if that is necessary. Hence calculating size() will typically be faster than storing it, but a constexpr implementation and compiler currently won't make that distinction.
None of which is an issue if a container is being entirely used within a constexpr function which has been determined to be evaluated at compile time. The problems occur when constexpr containers are used in runtime code, but certain functions such as size() are determined to be able to be evaluated at compile time, and therefore have their results cached. If there was a mechanism which specified that for a given class instance, it's constexpr functions may not be evaluated at compile time, then I would give the go-ahead. Or if there were a rule which stated that a class instance's member functions may only be evaluated at compile time if the class instance is entirely instantiated and destructed at compile time, I would give the go-ahead. This is not the situation we have as far as I can tell. If however my benchmark results above are in fact the result of compiler bugs, I will eat my words.
Time may sort these issues out, though I am personally happier for std::array and std::vector to be the "canaries in the coalmine" here. But I won't be recommending any change that produces, or can produce, on current compilers, a 2% performance decrease in runtime code, though I know the functionality of constexpr code is useful to some.
This proposal and it's reference implementation and the original reference implementation have several key differences, one is that the original is named 'colony', for historical and userbase reasons. Other differences follow:
"I'm the lead of the Editors team at Creative Assembly, where we make tools for the Total War series of games. The last game we released was Three Kingdoms, currently doing quite well on Steam. The main tool that I work on is the map creation editor, kind of our equivalent of Unreal Editor, so it's a big tool in terms of code size and complexity.
The way we are storing and rendering entities in the tool currently is very inefficient: essentially we have a quadtree which stores pointers to the entities, we query that quadtree to get a list of pointers to entities that are in the frustum, then we iterate through that list calling a virtual draw() function on each entity. Each part of that process is very cache-unfriendly: the quadtree itself is a cache-unfriendly structure, with nodes allocated on the heap, and the entities themselves are all over the place in memory, with a virtual function call on top.
So, I have made a new container class in which to store the renderable versions of the entities, and this class has a bunch of colonies inside, one for each type of 'renderable'. On top of this, instead of a quadtree, I now have a virtual quadtree. So each renderable contains the index of the quadtree node that it lives inside. Then, instead of asking the quadtree what entities are in the frustum, I ask the virtual quadtree for a node mask of the nodes what are in the frustum, which is just a bit mask. So when rendering, I iterate through all the renderables and just test the relevant bit of the node mask to see if the renderable is in the frustum. (Or more accurately, to see if the renderable has the potential to be in the frustum.) Nice and cache friendly.
When one adds an entity to the container, it returns a handle, which is just a pointer to the object inside one of the colonies returned as a std::uintptr_t. So I need this to remain valid until the object is removed, which is the other reason to use a colony."
"Just want to give you early heads up that I'm very interested in promoting the colony as part of Mongo for the project I'm designing now (not scheduled for execution yet), because it's the best container I found for pointer stable continuous memory."
"I'm using it as backing storage for a volumetric data structure (like openvdb). Its sparse so each tile is a 512^3 array of float voxels.
I thought that having colony will allow me to merge multiple grids together more efficiently as we can just splice the tiles and not copy or reallocate where the tiles dont overlap. Also adding and removing tiles will be fast. Its kind of like using an arena allocator or memory pool without having to actually write one."
Note: this is a private project Daniel is working on, not one for Weta Digital.
"Internally we use it as a slab allocator for objects with very different lifetime durations where we want aggressive hot memory reuse. It lets us ensure the algorithms are correct after the fact by being able to iterate over the container and verify what's alive.
It's a great single-type memory pool, basically, and it allows iteration for debugging purposes :)
Where it falls slightly short of expectation is having to iterate/delete/insert under a lock for multithreaded operation - for those usecases we had to do something different and lock-free, but for single-threaded applications it's amazing."