New Iterator Concepts
| Author: | David Abrahams, Jeremy Siek, Thomas Witt |
|---|---|
| Contact: | dave@boost-consulting.com, jsiek@osl.iu.edu, witt@acm.org |
| Organization: | Boost Consulting, Indiana University Open Systems Lab, University of Hanover Institute for Transport Railway Operation and Construction |
| Date: | 2003-09-22 |
| Number: | N1531=03-0114 |
| Copyright: | Copyright David Abrahams, Jeremy Siek, and Thomas Witt 2003. All rights reserved |
| Abstract: | We propose a new system of iterator concepts that treat access and positioning independently. This allows the concepts to more closely match the requirements of algorithms and provides better categorizations of iterators that are used in practice. This proposal is a revision of paper n1297 and n1477. |
|---|
- Motivation
- Impact on the Standard
- Design
- Proposed Text
- Addition to [lib.iterator.requirements]
- Iterator Value Access Concepts [lib.iterator.value.access]
- Iterator Traversal Concepts [lib.iterator.traversal]
- Incrementable Iterators [lib.incrementable.iterators]
- Single Pass Iterators [lib.single.pass.iterators]
- Forward Traversal Iterators [lib.forward.traversal.iterators]
- Bidirectional Traversal Iterators [lib.bidirectional.traversal.iterators]
- Random Access Traversal Iterators [lib.random.access.traversal.iterators]
- Addition to [lib.iterator.synopsis]
- Addition to [lib.iterator.traits]
- Addition to [lib.iterator.requirements]
Motivation
The standard iterator categories and requirements are flawed because they use a single hierarchy of concepts to address two orthogonal issues: iterator traversal and value access. As a result, many algorithms with requirements expressed in terms of the iterator categories are too strict. Also, many real-world iterators can not be accurately categorized. A proxy-based iterator with random-access traversal, for example, may only legally have a category of "input iterator", so generic algorithms are unable to take advantage of its random-access capabilities. The current iterator concept hierarchy is geared towards iterator traversal (hence the category names), while requirements that address value access sneak in at various places. The following table gives a summary of the current value access requirements in the iterator categories.
| Value Access Requirements in Existing Iterator Categories | |
|---|---|
| Output Iterator | *i = a |
| Input Iterator | *i is convertible to T |
| Forward Iterator | *i is T& (or const T& once issue 200 is resolved) |
| Random Access Iterator | i[n] is convertible to T (also i[n] = t is required for mutable iterators once issue 299 is resolved) |
Because iterator traversal and value access are mixed together in a single hierarchy, many useful iterators can not be appropriately categorized. For example, vector<bool>::iterator is almost a random access iterator, but the return type is not bool& (see issue 96 and Herb Sutter's paper J16/99-0008 = WG21 N1185). Therefore, the iterators of vector<bool> only meet the requirements of input iterator and output iterator. This is so nonintuitive that the C++ standard contradicts itself on this point. In paragraph 23.2.4/1 it says that a vector is a sequence that supports random access iterators.
Another difficult-to-categorize iterator is the transform iterator, an adaptor which applies a unary function object to the dereferenced value of the some underlying iterator (see transform_iterator). For unary functions such as times, the return type of operator* clearly needs to be the result_type of the function object, which is typically not a reference. Because random access iterators are required to return lvalues from operator*, if you wrap int* with a transform iterator, you do not get a random access iterator as might be expected, but an input iterator.
A third example is found in the vertex and edge iterators of the Boost Graph Library. These iterators return vertex and edge descriptors, which are lightweight handles created on-the-fly. They must be returned by-value. As a result, their current standard iterator category is input_iterator_tag, which means that, strictly speaking, you could not use these iterators with algorithms like min_element(). As a temporary solution, the concept Multi-Pass Input Iterator was introduced to describe the vertex and edge descriptors, but as the design notes for the concept suggest, a better solution is needed.
In short, there are many useful iterators that do not fit into the current standard iterator categories. As a result, the following bad things happen:
- Iterators are often mis-categorized.
- Algorithm requirements are more strict than necessary, because they cannot separate the need for random access or bidirectional traversal from the need for a true reference return type.
Impact on the Standard
The new iterator concepts are backward-compatible with the old iterator requirements, and old iterators are forward-compatible with the new iterator concepts. That is to say, iterators that satisfy the old requirements also satisfy appropriate concepts in the new system, and iterators modeling the new concepts will automatically satisfy the appropriate old requirements.
The algorithms in the standard library benefit from the new iterator concepts because the new concepts provide a more accurate way to express their type requirements. The result is algorithms that are usable in more situations and have fewer type requirements. The following lists the proposed changes to the type requirements of algorithms.
Forward Iterator -> Forward Traversal Iterator and Readable Iterator
find_end, adjacent_find, search, search_n, rotate_copy, lower_bound, upper_bound, equal_range, binary_search, min_element, max_element
Forward Iterator (1) -> Single Pass Iterator and Readable Iterator, Forward Iterator (2) -> Forward Traversal Iterator and Readable Iterator
find_first_of
Forward Iterator -> Readable Iterator and Writable Iterator
iter_swap
Forward Iterator -> Single Pass Iterator and Writable Iterator
fill, generate
Forward Iterator -> Forward Traversal Iterator and Swappable Iterator
rotate
Forward Iterator (1) -> Swappable Iterator and Single Pass Iterator, Forward Iterator (2) -> Swappable Iterator and Incrementable Iterator
swap_ranges
- Forward Iterator -> Forward Traversal Iterator and Readable Iterator and Writable Iterator
- remove, remove_if, unique
Forward Iterator -> Single Pass Iterator and Readable Iterator and Writable Iterator
replace, replace_if
- Bidirectional Iterator -> Bidirectional Traversal Iterator and Swappable Iterator
- reverse
- Bidirectional Iterator -> Bidirectional Traversal Iterator and Readable and Swappable Iterator
- partition
Bidirectional Iterator (1) -> Bidirectional Traversal Iterator and Readable Iterator, Bidirectional Iterator (2) -> Bidirectional Traversal Iterator and Writable Iterator
copy_backwards
- Bidirectional Iterator -> Bidirectional Traversal Iterator and Swappable Iterator and Readable Iterator
- next_permutation, prev_permutation
- Bidirectional Iterator -> Bidirectional Traversal Iterator and Readable Iterator and Writable Iterator
- stable_partition, inplace_merge
- Bidirectional Iterator -> Bidirectional Traversal Iterator and Readable Iterator
- reverse_copy
- Random Access Iterator -> Random Access Traversal Iterator and Readable and Writable Iterator
- random_shuffle, sort, stable_sort, partial_sort, nth_element, push_heap, pop_heap make_heap, sort_heap
- Input Iterator (2) -> Incrementable Iterator and Readable Iterator
- equal, mismatch
- Input Iterator (2) -> Incrementable Iterator and Readable Iterator
- transform
Design
The iterator requirements are to be separated into two groups. One set of concepts handles the syntax and semantics of value access:
- Readable Iterator
- Writable Iterator
- Swappable Iterator
- Lvalue Iterator
The access concepts describe requirements related to operator* and operator->, including the value_type, reference, and pointer associated types.
The other set of concepts handles traversal:
- Incrementable Iterator
- Single Pass Iterator
- Forward Traversal Iterator
- Bidirectional Traversal Iterator
- Random Access Traversal Iterator
The refinement relationships for the traversal concepts are in the following diagram.
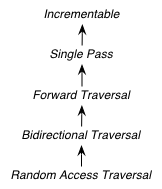
In addition to the iterator movement operators, such as operator++, the traversal concepts also include requirements on position comparison such as operator== and operator<. The reason for the fine grain slicing of the concepts into the Incrementable and Single Pass is to provide concepts that are exact matches with the original input and output iterator requirements.
The relationship between the new iterator concepts and the old are given in the following diagram.
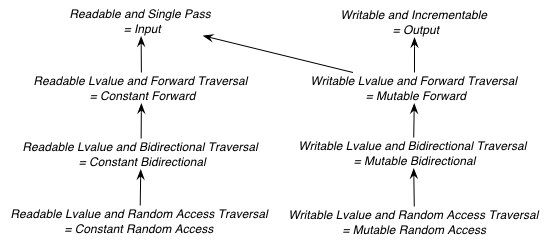
Like the old iterator requirements, we provide tags for purposes of dispatching based on the traversal concepts. The tags are related via inheritance so that a tag is convertible to another tag if the concept associated with the first tag is a refinement of the second tag. Since the access concepts are not related via refinement, but instead cover orthogonal issues, we do not use tags for the access concepts, but instead use the equivalent of a bit field.
We provide an access mechanism for mapping iterator types to the new traversal tags and access bit field. Our design reuses iterator_traits<Iter>::iterator_category as the access mechanism. To that end, the access and traversal information is bundled into a single type using the following iterator_tag class.
enum iterator_access { readable_iterator = 1, writable_iterator = 2,
swappable_iterator = 4, lvalue_iterator = 8 };
template <unsigned int access_bits, class TraversalTag>
struct iterator_tag : /* appropriate old category or categories */ {
static const iterator_access access =
(iterator_access)access_bits &
(readable_iterator | writable_iterator | swappable_iterator);
typedef TraversalTag traversal;
};
The access_bits argument is declared to be unsigned int instead of the enum iterator_access for convenience of use. For example, the expression (readable_iterator | writable_iterator) produces an unsigned int, not an iterator_access. The purpose of the lvalue_iterator part of the iterator_access enum is to communicate to iterator_tag whether the reference type is an lvalue so that the appropriate old category can be chosen for the base class. The lvalue_iterator bit is not recorded in the iterator_tag::access data member.
The iterator_tag class template is derived from the appropriate iterator tag or tags from the old requirements based on the access bits and traversal tag passed as template parameters. The algorithm for determining the old tag or tags picks the least-refined old concepts that include all of the requirements of the access and traversal concepts (that is, the closest fit), if any such category exists. For example, the category tag for a Readable Single Pass Iterator will always be derived from input_iterator_tag, while the category tag for a Single Pass Iterator that is both Readable and Writable will be derived from both input_iterator_tag and output_iterator_tag.
We also provide several helper classes that make it convenient to obtain the access and traversal characteristics of an iterator. These helper classes work both for iterators whose iterator_category is iterator_tag and also for iterators using the original iterator categories.
template <class Iterator> struct is_readable { typedef ... type; };
template <class Iterator> struct is_writable { typedef ... type; };
template <class Iterator> struct is_swappable { typedef ... type; };
template <class Iterator> struct traversal_category { typedef ... type; };
We do not include a helper class is_lvalue_iterator because that can easily be deduced by checking whether iterator_traits<Iterator>::reference is a real reference.
The most difficult design decision concerned the operator[]. The direct approach for specifying operator[] would have a return type of reference; the same as operator*. However, going in this direction would mean that an iterator satisfying the old Random Access Iterator requirements would not necessarily be a model of Readable or Writable Lvalue Iterator. Instead we have chosen a design that matches the preferred resolution of issue 299: operator[] is only required to return something convertible to the value_type (for a Readable Iterator), and is required to support assignment i[n] = t (for a Writable Iterator).
Proposed Text
Addition to [lib.iterator.requirements]
Iterator Value Access Concepts [lib.iterator.value.access]
In the tables below, X is an iterator type, a is a constant object of type X, T is std::iterator_traits<X>::value_type, and v is a constant object of type T.
Readable Iterators [lib.readable.iterators]
A class or built-in type X models the Readable Iterator concept for the value type T if the following expressions are valid and respect the stated semantics. U is the type of any specified member of type T.
| Readable Iterator Requirements (in addition to CopyConstructible) | ||
|---|---|---|
| Expression | Return Type | Note/Precondition |
| iterator_traits<X>::value_type | T | Any non-reference, non-cv-qualified type |
| iterator_traits<X>::reference | Convertible to iterator_traits<X>::value_type | |
| is_readable<X>::type | true_type | |
| *a | iterator_traits<X>::reference | pre: a is dereferenceable. If a == b then *a is equivalent to *b |
| a->m | U& | pre: (*a).m is well-defined. Equivalent to (*a).m |
Writable Iterators [lib.writable.iterators]
A class or built-in type X models the Writable Iterator concept if the following expressions are valid and respect the stated semantics. In addition, a model of Writable Iterator must include in its documentation the set of value types that it allows for output.
| Writable Iterator Requirements (in addition to CopyConstructible) | ||
|---|---|---|
| Expression | Return Type | Precondition |
| is_writable<X>::type | true_type | |
| *a = o | pre: The type of o is in the set of value types of X | |
Swappable Iterators [lib.swappable.iterators]
A class or built-in type X models the Swappable Iterator concept if the following expressions are valid and respect the stated semantics.
| Swappable Iterator Requirements (in addition to CopyConstructible) | ||
|---|---|---|
| Expression | Return Type | Postcondition |
| is_swappable<X>::type | true_type | |
| iter_swap(a, b) | void | the pointed to values are exchanged |
- [Note: An iterator that is a model of the Readable and Writable Iterator concepts
- is also a model of Swappable Iterator. --end note]
Lvalue Iterators [lib.lvalue.iterators]
The Lvalue Iterator concept adds the requirement that the reference type be a reference to the value type of the iterator.
| Lvalue Iterator Requirements | ||
|---|---|---|
| Expression | Return Type | Assertion |
| iterator_traits<X>::reference | T& | T is cv iterator_traits<X>::value_type where cv is an optional cv-qualification |
Iterator Traversal Concepts [lib.iterator.traversal]
In the tables below, X is an iterator type, a and b are constant objects of type X, r and s are mutable objects of type X, T is std::iterator_traits<X>::value_type, and v is a constant object of type T.
Incrementable Iterators [lib.incrementable.iterators]
A class or built-in type X models the Incrementable Iterator concept if the following expressions are valid and respect the stated semantics.
| Incrementable Iterator Requirements (in addition to Assignable, Copy Constructible) | ||
|---|---|---|
| Expression | Return Type | Assertion/Semantics |
| ++r | X& | &r == &++r |
| r++ | X |
{
X tmp = r;
++r;
return tmp;
}
|
| traversal_category<X>::type | Convertible to incrementable_iterator_tag | |
Single Pass Iterators [lib.single.pass.iterators]
A class or built-in type X models the Single Pass Iterator concept if the following expressions are valid and respect the stated semantics.
| Single Pass Iterator Requirements (in addition to Incrementable Iterator and Equality Comparable) | ||
|---|---|---|
| Expression | Return Type | Assertion/Semantics / Pre-/Post-condition |
| ++r | X& | pre: r is dereferenceable; post: r is dereferenceable or r is past-the-end |
| a == b | convertible to bool | == is an equivalence relation over its domain |
| a != b | convertible to bool | !(a == b) |
| traversal_category<X>::type | Convertible to single_pass_iterator_tag | |
Forward Traversal Iterators [lib.forward.traversal.iterators]
A class or built-in type X models the Forward Traversal Iterator concept if the following expressions are valid and respect the stated semantics.
| Forward Traversal Iterator Requirements (in addition to Single Pass Iterator) | ||
|---|---|---|
| Expression | Return Type | Assertion/Note |
| X u; | X& | note: u may have a singular value. |
| ++r | X& | r == s and r is dereferenceable implies ++r == ++s. |
| iterator_traits<X>::difference_type | A signed integral type representing the distance between iterators | |
| traversal_category<X>::type | Convertible to forward_traversal_iterator_tag | |
Bidirectional Traversal Iterators [lib.bidirectional.traversal.iterators]
A class or built-in type X models the Bidirectional Traversal Iterator concept if the following expressions are valid and respect the stated semantics.
| Bidirectional Traversal Iterator Requirements (in addition to Forward Traversal Iterator) | ||
|---|---|---|
| Expression | Return Type | Assertion/Semantics / Pre-/Post-condition |
| --r | X& | pre: there exists s such that r == ++s. post: s is dereferenceable. --(++r) == r. --r == --s implies r == s. &r == &--r. |
| r-- | convertible to const X& |
{
X tmp = r;
--r;
return tmp;
}
|
| traversal_category<X>::type | Convertible to bidirectional_traversal_iterator_tag | |
Random Access Traversal Iterators [lib.random.access.traversal.iterators]
A class or built-in type X models the Random Access Traversal Iterator concept if the following expressions are valid and respect the stated semantics. In the table below, Distance is iterator_traits<X>::difference_type and n represents a constant object of type Distance.
| Random Access Traversal Iterator Requirements (in addition to Bidirectional Traversal Iterator) | |||
|---|---|---|---|
| Expression | Return Type | Operational Semantics | Assertion/ Precondition |
| r += n | X& |
{
Distance m = n;
if (m >= 0)
while (m--)
++r;
else
while (m++)
--r;
return r;
}
|
|
| a + n, n + a | X | { X tmp = a; return tmp += n; } | |
| r -= n | X& | return r += -n | |
| a - n | X | { X tmp = a; return tmp -= n; } | |
| b - a | Distance | a < b ? distance(a,b) : -distance(b,a) | pre: there exists a value n of Distance such that a + n == b. b == a + (b - a). |
| a[n] | convertible to T | *(a + n) | pre: a is a readable iterator |
| a[n] = v | convertible to T | *(a + n) = v | pre: a is a writable iterator |
| a < b | convertible to bool | b - a > 0 | < is a total ordering relation |
| a > b | convertible to bool | b < a | > is a total ordering relation |
| a >= b | convertible to bool | !(a < b) | |
| a <= b | convertible to bool | !(a > b) | |
| traversal_category<X>::type | Convertible to random_access_traversal_iterator_tag | ||
Addition to [lib.iterator.synopsis]
// lib.iterator.traits, traits and tags
template <class Iterator> struct is_readable;
template <class Iterator> struct is_writable;
template <class Iterator> struct is_swappable;
template <class Iterator> struct traversal_category;
enum iterator_access { readable_iterator = 1, writable_iterator = 2,
swappable_iterator = 4, lvalue_iterator = 8 };
template <unsigned int access_bits, class TraversalTag>
struct iterator_tag : /* appropriate old category or categories */ {
static const iterator_access access =
(iterator_access)access_bits &
(readable_iterator | writable_iterator | swappable_iterator);
typedef TraversalTag traversal;
};
struct incrementable_iterator_tag { };
struct single_pass_iterator_tag : incrementable_iterator_tag { };
struct forward_traversal_tag : single_pass_iterator_tag { };
struct bidirectional_traversal_tag : forward_traversal_tag { };
struct random_access_traversal_tag : bidirectional_traversal_tag { };
struct null_category_tag { };
struct input_output_iterator_tag : input_iterator_tag, output_iterator_tag {};
Addition to [lib.iterator.traits]
The iterator_tag class template is an iterator category tag that encodes the access enum and traversal tag in addition to being compatible with the original iterator tags. The iterator_tag class inherits from one of the original iterator tags according to the following pseudo-code.
inherit-category(access, traversal-tag) =
if ((access & readable_iterator) && (access & lvalue_iterator)) {
if (traversal-tag is convertible to random_access_traversal_tag)
return random_access_iterator_tag;
else if (traversal-tag is convertible to bidirectional_traversal_tag)
return bidirectional_iterator_tag;
else if (traversal-tag is convertible to forward_traversal_tag)
return forward_iterator_tag;
else if (traversal-tag is convertible to single_pass_traversal_tag)
if (access-tag is convertible to writable_iterator_tag)
return input_output_iterator_tag;
else
return input_iterator_tag;
else
return null_category_tag;
} else if ((access & readable_iterator) and (access & writable_iterator)
and traversal-tag is convertible to single_pass_iterator_tag)
return input_output_iterator_tag;
else if (access & readable_iterator
and traversal-tag is convertible to single_pass_iterator_tag)
return input_iterator_tag;
else if (access & writable_iterator
and traversal-tag is convertible to incrementable_iterator_tag)
return output_iterator_tag;
else
return null_category_tag;
If the argument for TraversalTag is not convertible to incrementable_iterator_tag then the program is ill-formed.
The is_readable, is_writable, is_swappable, and traversal_category class templates are traits classes. For iterators whose iterator_traits<Iter>::iterator_category type is iterator_tag, these traits obtain the access enum and traversal member type from within iterator_tag. For iterators whose iterator_traits<Iter>::iterator_category type is not iterator_tag and instead is a tag convertible to one of the original tags, the appropriate traversal tag and access bits are deduced. The following pseudo-code describes the algorithm.
is-readable(Iterator) =
cat = iterator_traits<Iterator>::iterator_category;
if (cat == iterator_tag<Access,Traversal>)
return Access & readable_iterator;
else if (cat is convertible to input_iterator_tag)
return true;
else
return false;
is-writable(Iterator) =
cat = iterator_traits<Iterator>::iterator_category;
if (cat == iterator_tag<Access,Traversal>)
return Access & writable_iterator;
else if (cat is convertible to forward_iterator_tag
or output_iterator_tag)
return true;
else
return false;
is-swappable(Iterator) =
cat = iterator_traits<Iterator>::iterator_category;
if (cat == iterator_tag<Access,Traversal>)
return Access & swappable_iterator;
else if (cat is convertible to forward_iterator_tag) {
if (iterator_traits<Iterator>::reference is a const reference)
return false;
else
return true;
} else
return false;
traversal-category(Iterator) =
cat = iterator_traits<Iterator>::iterator_category;
if (cat == iterator_tag<Access,Traversal>)
return Traversal;
else if (cat is convertible to random_access_iterator_tag)
return random_access_traversal_tag;
else if (cat is convertible to bidirectional_iterator_tag)
return bidirectional_traversal_tag;
else if (cat is convertible to forward_iterator_tag)
return forward_traversal_tag;
else if (cat is convertible to input_iterator_tag)
return single_pass_iterator_tag;
else if (cat is convertible to output_iterator_tag)
return incrementable_iterator_tag;
else
return null_category_tag;
The following specializations provide the access and traversal category tags for pointer types.
template <typename T>
struct is_readable<const T*> { typedef true_type type; };
template <typename T>
struct is_writable<const T*> { typedef false_type type; };
template <typename T>
struct is_swappable<const T*> { typedef false_type type; };
template <typename T>
struct is_readable<T*> { typedef true_type type; };
template <typename T>
struct is_writable<T*> { typedef true_type type; };
template <typename T>
struct is_swappable<T*> { typedef true_type type; };
template <typename T>
struct traversal_category<T*>
{
typedef random_access_traversal_tag type;
};